练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (17)如图，在△ABC中，AC=2，BC=1，cosC=．

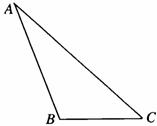
    (Ⅰ)求AB的值；

    (Ⅱ)求sin(2A+C)的值．

    本小题考查同角三角函数关系、两角和公式、倍角公式、正弦定理、余弦定理等基础知识，考查基本运算能力及分析和解决问题的能力．

        (Ⅰ)解：由余弦定理，

        AB2=AC2+BC2-2AC·BCcosC

           =4+1-2×2×1×=2．

    那么，AB=．

    (Ⅱ)解：由cosC=且0＜C＜π，得sinC=由正弦定理，

    ,

    解得sinA=,所以,cosA=.由倍角公式

    sin2A=2sinA·cosA=，

    且cos2A=1-2sin2A=，故

    sin（2A+C）=sin2AcosC+cos2AsinC=.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    4、某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：每一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；…第六组，成绩大于等于18秒且小于等于19秒．如图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班人数的百分比为x，成绩大于等于15秒且小于17秒的学生人数为y，则从频率分布直方图中可以分析出x和y分别为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图所示，矩形长为6，宽为4，在矩形内随机的撒2400颗黄豆，数得落在椭圆外的黄豆数为516颗，依据此实验数据可以估计出椭圆的面积约为（　　）
    A、5.16B、6.16C、18.84D、17.84

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，直线l1和l2相交于点M且l1⊥l2，点N∈l1．以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=
    		17
    ，|AN|=3，且|BN|=6．
    （1）曲线段C是哪类圆锥曲线的一部分？并建立适当的坐标系，求曲线段C所在的圆锥曲线的标准方程；
    （2）在（1）所建的坐标系下，已知点P（m，n）在曲线段C上，直线l：mx+ny=1，求直线l被圆x2+y2=1截得的弦长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

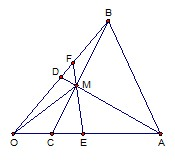    如图，在△ABO中，
    OC
    =
    1
    4
    OA
    ，
    OD
    =
    1
    2
    OB
    ，AD交BC于M，设
    OA
    =
    a
    ，
    OB
    =
    b
    ．
    ①用
    a
    、
    b
    表示
    OM
    ；
    ②在线段AC上取一点E，线段BD上取一点F，使EF过M点，设
    OE
    =λ
    OA
    ，
    OF
    =μ
    OB
    ．
    求证：
    1
    7λ
    +
    3
    7μ
    =1    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

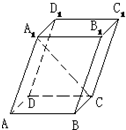    精英家教网如图，在平行六面体ABCD-A1B1C1D1中，底面是边长为2的正方形，若∠A1AB=∠A1AD=60°，且A1A=3，则A1C的长为（　　）
    A、
    		5
    B、2
    		2
    C、
    		14
    D、
    		17

    查看答案和解析>>

    同步练习册答案