Question

【题目】已知椭圆C： + =1（a＞b＞D）的离心率为 ，过右焦点F的直线l与C相交于A、B两点，当l的斜率为1时，坐标原点O到l的距离为 ．
（1）求a、b的值；
（2）C上是否存在点P，使得当l绕P转到某一位置时，有 = + 成立？若存在，求出所有的P的坐标与l的方程；若不存在，说明理由．

Answer 1

【答案】
（1）解：直线l的方程为y=x﹣c，则 = ，解得c=1，

又 ，b2=a2﹣c2，解得 ，b2=2．

∴得 ，b=

（2）解：由（1）可得：椭圆C的方程为 =1．

假设C上存在点P，使得当l绕P转到某一位置时，有 = + 成立．设A（x1，y1），B（x2，y2）．

设直线l的方程为my=x﹣1，联立 ，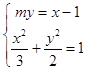

化为（2m2+3）y2+4my﹣4=0，

∴y1+y2= ．

∴x1+x2=m（y1+y2）+2= ．

∴ = + =（x1+x2，y1+y2）= ．

代入椭圆方程可得： + =1，

化为2m2﹣1=0，

解得m= ．

∴直线l的方程为：y= （x﹣1）．

由方程： ﹣1=0，

解得 ， ， ， ．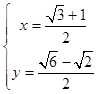

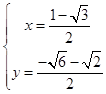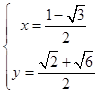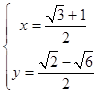因此假设正确

【解析】（1）直线l的方程为y=x﹣c，则 = ，解得c，又 ，b2=a2﹣c2，解得a，b即可得出．（2）由（1）可得：椭圆C的方程为 =1．假设C上存在点P，使得当l绕P转到某一位置时，有 = + 成立．设A（x1，y1），B（x2，y2）．

设直线l的方程为my=x﹣1，与椭圆方程联立化为（2m2+3）y2+4my﹣4=0，利用根与系数的关系及其 = + =（x1+x2，y1+y2），可得点P的坐标（用m表示），代入椭圆的方程即可得出．