
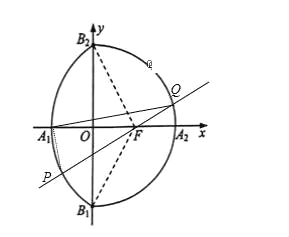
����Ŀ���Ѱ���Բ![]() ��x��0����Բ����x��c��2+y2=a2��x��0���ϳɵ����߳�������Բ��������F��c��0��Ϊ����Բ���ҽ��㣮��ͼ��A1��A2��B1��B2�ֱ�������Բ����x�ᡢy��Ľ��㣬��֪��B1FB2=
��x��0����Բ����x��c��2+y2=a2��x��0���ϳɵ����߳�������Բ��������F��c��0��Ϊ����Բ���ҽ��㣮��ͼ��A1��A2��B1��B2�ֱ�������Բ����x�ᡢy��Ľ��㣬��֪��B1FB2=![]() ������FB1A1B2�����Ϊ
������FB1A1B2�����Ϊ![]() ��
��
��1����a��c��ֵ��
��2������F����б��Ϊ����ֱ�߽�����Բ����P��Q���㣬�Խ���A1PQ���ܳ�L��ʾΪ���ĺ�����
��3���ڣ�2���������£�����A1PQ���ܳ�Lȡ�����ֵʱ����̽����A1PQ������Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ�����������ȡֵ��Χ��
-��
���𰸡���1��a=2��c=1����2������������3��![]() .
.
��������
��1��������Բ��������![]() ���������������ʽ������з��̿����
���������������ʽ������з��̿����![]() ��ֵ.����
��ֵ.����![]() �����
�����![]() ��ֵ��2���ɣ�1���Ľ��������Բ�ķ��̺�Բ�ķ���.��
��ֵ��2���ɣ�1���Ľ��������Բ�ķ��̺�Բ�ķ���.��![]() �ֳ�
�ֳ�![]() ���࣬������Բ�Ķ���ͽ�������������������
���࣬������Բ�Ķ���ͽ�������������������![]() ���ܳ�.��3���ɣ�2���ķ�����֪��������
���ܳ�.��3���ɣ�2���ķ�����֪��������![]() ���ȡ�����ֵʱ��
���ȡ�����ֵʱ��![]() �ڰ���Բ��.�����ҳ���ʽ���
�ڰ���Բ��.�����ҳ���ʽ���![]() �ij������õ㵽ֱ�ߵľ��빫ʽ���
�ij������õ㵽ֱ�ߵľ��빫ʽ���![]() ��
��![]() �ľ��룬�г�������
�ľ��룬�г�������![]() ����ı���ʽ�����û�Ԫ����������ȡֵ��Χ.
����ı���ʽ�����û�Ԫ����������ȡֵ��Χ.
��1��������Բ��������![]() ���������������ʽ��
���������������ʽ��![]() ������
������![]() ����
����![]() .
.
��2���ɣ�1��֪![]() ���ʰ���Բ����Ϊ
���ʰ���Բ����Ϊ![]() ��Բ���ķ���Ϊ
��Բ���ķ���Ϊ![]() .��
.��![]() ǡ������Բ����.��Ȼֱ��
ǡ������Բ����.��Ȼֱ��![]() ��б�ʲ���Ϊ
��б�ʲ���Ϊ![]() ������
������![]() �ķ���Ϊ
�ķ���Ϊ![]() .�ٵ�
.�ٵ�![]() ʱ��
ʱ��![]() �ֱ���Բ���Ͱ���Բ�ϣ�
�ֱ���Բ���Ͱ���Բ�ϣ�![]() Ϊ��Ϊ
Ϊ��Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�![]() ����
����![]() ���ܳ�
���ܳ�![]()
�ڵ�![]() ʱ��
ʱ��![]() �ֱ�Բ���Ͱ���Բ�ϣ�ͬ���ٿ����
�ֱ�Բ���Ͱ���Բ�ϣ�ͬ���ٿ����![]() ���ܳ�
���ܳ�![]() .
.
�۵�![]() ʱ��
ʱ��![]() ���ڰ���Բ�ϣ���ʱ
���ڰ���Բ�ϣ���ʱ![]() ���ܳ�
���ܳ�![]() .
.
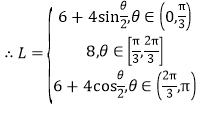
��3���ɣ�2��֪����![]() ���ڰ���Բ��ʱ��
���ڰ���Բ��ʱ��![]() ���ܳ�ȡ�����ֵ.��ֱ��
���ܳ�ȡ�����ֵ.��ֱ��![]() �ķ��̴�����Բ���̲������
�ķ��̴�����Բ���̲������![]() ������
������![]() �����ҳ���ʽ��
�����ҳ���ʽ��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ����������
����������![]() �����
�����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϵ�������
�ϵ�������![]() ������
������![]() .
.


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ƽ��ʾ��ͼΪ����ͼ���������ABCDE����������������ABEΪ���������ı�������BCDEΪ��ѧ����AB��BC��CD��DE��EA��BEΪѧУ����Ҫ��·�������ǿ��ȣ�. ![]() ��
�� ![]() ��
�� 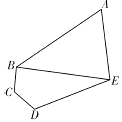
��1�����·BE�ij��ȣ�
��2������������ABE��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C����ABΪֱ����ԲO������A��B�ĵ㣬ƽ��PAC��ƽ��ABC��PA=PC=AC=2��BC=4��E��F �ֱ���PC��PB���е㣬��ƽ��AEF��ƽ��ABC�Ľ���Ϊֱ��l��
������֤��ֱ��l��ƽ��PAC��
����ֱ��l���Ƿ���ڵ�Q��ʹֱ��PQ�ֱ���ƽ��AEF��ֱ��EF���ɵĽǻ��ࣿ�����ڣ����|AQ|��ֵ���������ڣ���˵�����ɣ�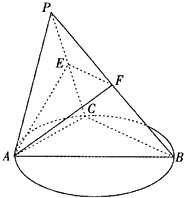
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪����f��x��=ax3+bx2��ͼ����M��1��4���������ڵ�M��������ǡ����ֱ��x+9y��3=0��ֱ��
��1����ʵ��a��b��ֵ
��2��������f��x��������[m��m+1]�ϵ�����������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��2a|+|x+ ![]() |
|
��1����a=1ʱ����ʽf��x����4�Ľ⼯��
��2��������ʽf��x����m2��m+2 ![]() ������ʵ��x��a���������ʵ��m��ȡֵ��Χ��
������ʵ��x��a���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�������������տ������˻ῪĻʽ����ij���߷ֱ��ij����60��70�꣬40��50�꣬20��30�������������е�160�ˣ�240�ˣ�x���У����÷ֲ�����ķ����������30�˽��е��飬����60��70�����������г����8�ˣ���ôxΪ(����) ��
A. 90 B. 120 C. 180 D. 200
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ�ij���������ȡ���ָ߶�ѧ��,�����䵽У�����ʱ��(��λ:����),�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ(��ͼ),���е�У����ʱ��ķ�Χ��![]() ,�������ݷ���Ϊ
,�������ݷ���Ϊ![]() .
.

(1)��ֱ��ͼ��![]() ��ֵ��
��ֵ��
(2)���ѧ����У����ʱ�䲻����1Сʱ,���������ѧУס��.����У¼ȡ1200������,����Ƹ߶��������ж����˿�������ס�ޣ�
(3)��ֱ��ͼ�е�Ƶ����Ϊ����,�ִӸ�ѧУ�ĸ߶���������ѡ4��ѧ��,��![]() ��ʾ��ѡ4��ѧ���С���У����ʱ������40���ӡ�������,��
��ʾ��ѡ4��ѧ���С���У����ʱ������40���ӡ�������,��![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����dz����ƺ��������ʽ![]() ��
��![]() �����ҽ���
�����ҽ���![]() ʱ�Ⱥų���)Ϊ����겻��ʽ�������ڴ��������뵼�������г���������Ҫ����.
ʱ�Ⱥų���)Ϊ����겻��ʽ�������ڴ��������뵼�������г���������Ҫ����.
��1����֤���������ʽ��
��2���躯��![]() �����ڶ������ں���
�����ڶ������ں���![]() ����ʵ��
����ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2x�����㣨2��0����ֱ��l��C��A��B���㣬ԲM�����߶�ABΪֱ����Բ��
����֤��������ԭ��O��ԲM�ϣ�
������ԲM����P��4����2������ֱ��l��ԲM�ķ��̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com