
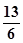 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+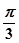 )的值.
)的值.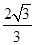 (2)
(2)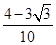
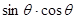 的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件:
的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件: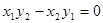 可得
可得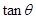 的值,法一:由
的值,法一:由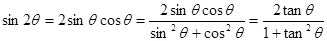 (万能公式)得到
(万能公式)得到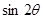 的值,同理可得
的值,同理可得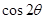 的值;再利用正弦和角公式将sin(2θ+
的值;再利用正弦和角公式将sin(2θ+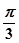 )展开即可求得其值;法二:也可由
)展开即可求得其值;法二:也可由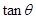 的值,应用三角函数的定义求得
的值,应用三角函数的定义求得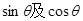 的值,进而用倍角公式可求得
的值,进而用倍角公式可求得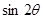 和
和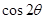 的值,下同法一.
的值,下同法一.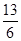 ,所以sinθcosθ=
,所以sinθcosθ=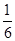 .
.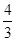 .
.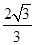 .
.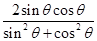 =
=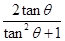 =
=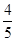 ,
,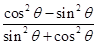 =
=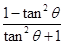 =-
=-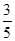 .
.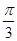 )=
)=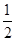 sin2θ+
sin2θ+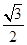 cos2θ=
cos2θ=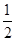 ×
×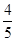 +
+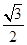 ×(-
×(-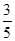 )=
)=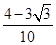 .
.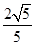 ,cosθ=
,cosθ=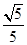 .
.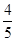 , cos2θ=cos2θ-sin2θ=-
, cos2θ=cos2θ-sin2θ=-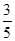 .
.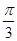 )=
)=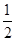 sin2θ+
sin2θ+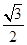 cos2θ=
cos2θ=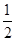 ×
×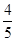 +
+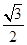 ×(-
×(-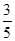 )=
)=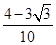 .
. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com