【题目】已知
，函数
.
（1）当
时，在给出的坐标系中，画出函数
的大致图象，根据图象写出函数的单调减区间；
（2）讨论关于
的方程
解的个数.
【答案】（1）
的单调递减区间是
;（2）当
时, 关于
的方程
解有1个; 当
或
时，关于的方程解有2个;当
或
时, 关于的方程解有3个.
【解析】
（1）去绝对值转化为分段函数,即可作出函数的图像,根据图像求出单调递减区间;
（2）关于的方程解的个数等价于
于直线
的图像交点个数.
（1）当时，
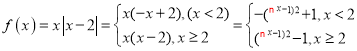
其图像为：
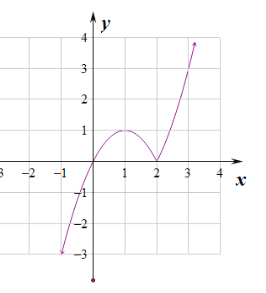
根据图像的单调递减区间是.
（2）依题意，关于关于的方程解的个数等价于于直线的图像交点个数. 
当且仅当是等号成立，
所以当
，即时，于直线的图像有1个交点;
当或时，于直线的图像2个交点;
当或时，于直线的图像3个交点;
所以当时, 关于的方程解有1个; 当或时，关于的方程解有2个;当或时, 关于的方程解有3个.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A(0，3)，直线l：y＝2x－4，设圆C的半径为1，圆心C在直线l上，若圆C上存在点M，使|MA|＝2|MO|，则点M的轨迹方程是________，圆心C的横坐标的取值范围是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】手机完全充满电量，在开机不使用的状态下，电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间．
为了解
， 
两个不同型号手机的待机时间，现从某卖场库存手机中随机抽取
， 
两个型号的手机各
台，在相同条件下进行测试，统计结果如下，
手机编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中， 
， 
是正整数，且
．
（
）该卖场有
台
型手机，试估计其中待机时间不少于
小时的台数．
（
）从
型号被测试的
台手机中随机抽取
台，记待机时间大于
小时的台数为
，求
的分布列及其数学期望．
（
）设
， 
两个型号被测试手机待机时间的平均值相等，当
型号被测试手机待机时间的方差最小时，写出
， 
的值（结论不要求证明）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度，某中学团委以问卷形式调查了
位家长，得到如下统计表：
（1）据此样本，能否有
的把握认为“接受程度”与家长性别有关？说明理由；
（2）学校决定从男性家长中按分层抽样方法选出
人参加今年的高中学生成人礼仪式，并从中选
人交流发言，设
是发言人中持“赞成”态度的人数，求
的分布列及数学期望.
参考数据
|
|
|
|
|
|
参考公式
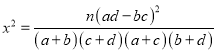
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题错误的是( )
A. 若p∨q为假命题，则p∧q为假命题
B. 若a，b∈[0,1]，则不等式a2＋b2<
成立的概率是
C. 命题“x∈R，使得x2＋x＋1<0”的否定是“x∈R，x2＋x＋1≥0”
D. 已知函数f(x)可导，则“f′(x0)＝0”是“x0是函数f(x)的极值点”的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
