
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
【答案】
(1)解:∵f(xy)=f(x)+f(y),f(2)=1.
∴f(4)=f(2×2)=f(2)+f(2)=2
∴f(8)=f(4×2)=f(4)+f(2)=3
(2)解:根据题意,不等式f(x)﹣f(x﹣2)>3可变为
f(x)>f(x﹣2)+3=f(x﹣2)+f(8)=f[8(x﹣2)]
∵f(x)在(0,+∞)上是增函数, 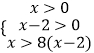 ,
,
解得 ![]() ,
,
∴原不等式的解集是 ![]()
【解析】(1)直接把4分成2×2,再代入f(xy)=f(x)+f(y),结合f(2)=1即可求出f(4)的值,同理可得f(8)的值;(2)先把不等式f(x)﹣f(x﹣2)>3转化为f(x)>f(x﹣2)+3=f(x﹣2)+f(8)=f[8(x﹣2)];再结合f(x)是定义在(0,+∞)上的增函数即可求出不等式的解集.(注意其定义域的限制)


科目:高中数学 来源: 题型:
【题目】对于x∈R,[x]表示不超过x的最整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤ ![]() },则A中所有元素的和为( )
},则A中所有元素的和为( )
A.15
B.19
C.20
D.55
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在 ![]() 轴上的圆
轴上的圆 ![]() 过点
过点 ![]() 和
和 ![]() ,圆
,圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)由圆 ![]() 上的动点
上的动点 ![]() 向圆
向圆 ![]() 作两条切线分别交
作两条切线分别交 ![]() 轴于
轴于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F. 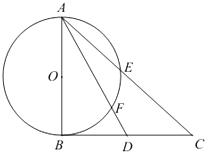
(1)证明:C,E,F,D四点共圆;
(2)若D为BC的中点,且AF=3,FD=1,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)+2= ![]() ,当x∈(0,1]时,f(x)=x2 , 若在区间(﹣1,1]内,g(x)=f(x)﹣t(x+2)有两个不同的零点,则实数t的取值范围是( )
,当x∈(0,1]时,f(x)=x2 , 若在区间(﹣1,1]内,g(x)=f(x)﹣t(x+2)有两个不同的零点,则实数t的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com