已知等比数列{an}的公比为q(q≠1)的等比数列,且a2011,a2013,a2012成等差数列.
(Ⅰ)求公比q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
【答案】
分析:(Ⅰ)由数列{a
n}是公比为q(q≠1)的等比数列,结合a
2011,a
2013,a
2012成等差数列,直接利用等差数列的性质列式进行计算;
(Ⅱ)求出等差数列{b
n}的前n项和,由S
n与b
n作差得到S
n-1,代入前n-1项和的表达式后因式分解,然后分类讨论比较
S
n与b
n的大小.
解答:解答:(Ⅰ)由数列{a
n}是公比为q(q≠1)的等比数列,且a
2011,a
2013,a
2012成等差数列,
所以2a
2013=a
2011+a
2012,即
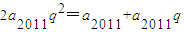
,
∵a
2011≠0,∴2q
2-q-1=0.
∴q=1或
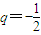
,
又q≠1,∴
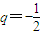
;
(Ⅱ)数列{b
n}是以2为首项,q为公差的等差数列,
公差
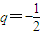
,则
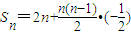
=
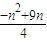
.
当n≥2时,

=
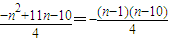
,
故对于n∈N
*,当2≤n≤9时,S
n>b
n;
当n=10时,S
n=b
n;
当n≥11时,S
n<b
n.
点评:本题是等差数列和等比数列的综合题,考查了等差数列的性质,考查了等差数列的前n项和,训练了作差法比较两个数的大小,利用了分类讨论的数学思想方法,是中档题.

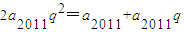 ,
,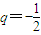 ,
,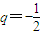 ;
;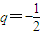 ,则
,则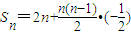 =
=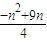 .
.
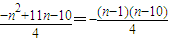 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案