
【题目】已知边长为![]() 的正
的正![]() 的顶点
的顶点![]() 在平面
在平面![]() 内,顶点
内,顶点![]() ,
,![]() 在平面
在平面![]() 外的同一侧,点
外的同一侧,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 在平面
在平面![]() 内的投影,设
内的投影,设![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .若
.若![]() 是以角
是以角![]() 为直角的直角三角形,则
为直角的直角三角形,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】分析:由题意找出线面角,设BB′=a,CC′=b,可得ab=2,然后由a的变化得到A′B′的变化范围,从而求得tanφ的范围.
详解:如图,
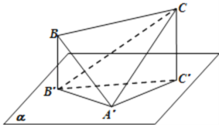
由CC′⊥α,A′B′α,得A′B′⊥CC′,
又A′B′⊥A′C′,且A′C′∩CC′=C′,
∴A′B′⊥面A′C′C,则φ=∠B′CA′,
设BB′=a,CC′=b,则A′B′2=4﹣a2,A′C′2=4﹣b2,
设B′C′=c,
则有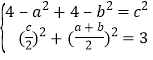 ,整理得:ab=2.
,整理得:ab=2.
∵|BB′|≤|CC′|,∴a≤b,
tanφ=![]() ,
,
在三角形BB′A′中,∵斜边A′B为定值2,
∴当a最大为![]() 时,A′B′取最小值
时,A′B′取最小值![]() ,tanφ的最小值为
,tanφ的最小值为![]() .
.
当a减小时,tanφ增大,
若a≤1,则b≥2,在Rt△A′CC′中出现直角边大于等于斜边,矛盾,
∴a>1,此时A′B′<![]() ,即tanφ
,即tanφ![]() .
.
∴tanφ的范围为![]() .即
.即![]() 的最小值为
的最小值为![]()
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 过点
过点 ![]() ,左右焦点为F1(﹣c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
,左右焦点为F1(﹣c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.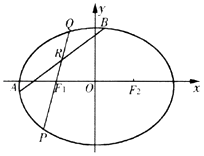
(I)求椭圆C方程;
(II)圆D: ![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2cos2x的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
个单位后得到函数g(x)的图象,若函数g(x)在区间[0, ![]() ]和[2a,
]和[2a, ![]() ]上均单调递增,则实数a的取值范围是( )
]上均单调递增,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,其中
,其中![]() 点在
点在![]() 点上方,直角顶点
点上方,直角顶点![]() 的坐标为
的坐标为![]() .
.

(1)求![]() 边上的高线
边上的高线![]() 所在直线的方程;
所在直线的方程;
(2)求等腰直角三角形![]() 的外接圆的标准方程;
的外接圆的标准方程;
(3)分别求两直角边![]() ,
,![]() 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在道路边安装路灯,路面![]() 宽
宽![]() ,灯柱
,灯柱![]() 高14
高14![]() ,灯杆
,灯杆![]() 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直,轴线
垂直,轴线![]() ,灯杆
,灯杆![]() 都在灯柱
都在灯柱![]() 和路面宽线
和路面宽线![]() 确定的平面内.
确定的平面内.

(1)当灯杆![]() 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线![]() 正好通过路面
正好通过路面![]() 的中线?
的中线?
(2)如果灯罩轴线AC正好通过路面![]() 的中线,此时有一高2.5
的中线,此时有一高2.5 ![]() 的警示牌直立在
的警示牌直立在![]() 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制造商![]() 月生产了一批乒乓球,随机抽样
月生产了一批乒乓球,随机抽样![]() 个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |

(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com