
 (
(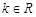 ).
).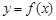 在
在 处取得极大值,求
处取得极大值,求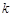 的值;
的值;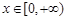 时,函数
时,函数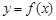 图象上的点都在
图象上的点都在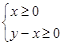 所表示的区域内,求
所表示的区域内,求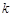 的取值范围;
的取值范围;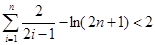 ,
,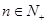 .
.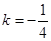 ;(2)
;(2) 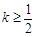 .
.  ,
,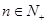 。
。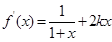 ,由
,由 经检验符合题意 (3分)
经检验符合题意 (3分) 在
在 恒成立.令
恒成立.令 ,
,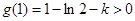 ,故k≤0不合.(4分)
,故k≤0不合.(4分) -2kx=
-2kx=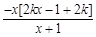 .
.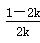 >-1. (5分)
>-1. (5分)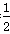 时,
时,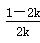 ≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,故k≥
≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,故k≥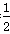 符合题意,6分②当0<k<
符合题意,6分②当0<k<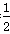 时,
时,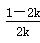 >0, 对于x∈
>0, 对于x∈ ,g′(x)>0,
,g′(x)>0, 内单调递增,因此当取x0∈
内单调递增,因此当取x0∈ 时,g(x0)>g(0)=0,不合.
时,g(x0)>g(0)=0,不合.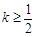 . (8分)
. (8分)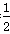 ,得
,得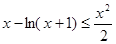 (10分)
(10分) 代入上式得:
代入上式得: 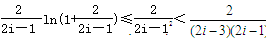 (12分)
(12分)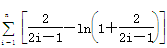 ≤2-ln3+
≤2-ln3+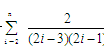
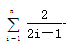 -ln(2n+1)≤2-ln3+1-
-ln(2n+1)≤2-ln3+1-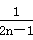 <2.
<2. ,
,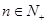 (14分)
(14分)

科目:高中数学 来源:不详 题型:解答题
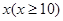 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为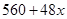 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
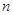 个月的维修费为
个月的维修费为 元,买这种冰激凌机花费
元,买这种冰激凌机花费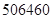 元,使用
元,使用 年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( )
年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( ) 机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;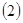 一年按
一年按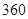 天计算.)
天计算.)A.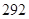 元 元 | B.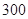 元 元 | C.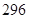 元 元 | D.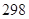 元 元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的函数
的函数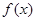 ,定义
,定义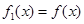 ,
,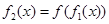 ,…,
,…,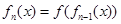 ,n=1,2,3,….满足
,n=1,2,3,….满足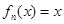 的点称为f的
的点称为f的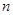 阶周期点.
阶周期点.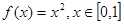 则f的
则f的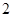 阶周期点的个数是___________;
阶周期点的个数是___________;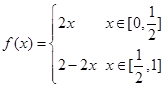 则f的
则f的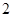 阶周期点的个数是__________ .
阶周期点的个数是__________ .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com