
【题目】已知棱长为2的正方体![]() 中,E为DC中点,F在线段
中,E为DC中点,F在线段![]() 上运动,则三棱锥
上运动,则三棱锥![]() 的外接球的表面积最小值为( )
的外接球的表面积最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
取![]() 的中点
的中点![]() ,易知
,易知![]() 为
为![]() 的外心,取
的外心,取![]() 的中点
的中点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,由正方体的性质可得三棱锥
,由正方体的性质可得三棱锥![]() 的外接球球心
的外接球球心![]() 在直线
在直线![]() 上,连接
上,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,易知当
,易知当![]() 即点
即点![]() 与
与![]() 重合时,
重合时,![]() 即外接球半径最小,设
即外接球半径最小,设![]() ,根据
,根据![]() 求得
求得![]() ,进而可求得外接球半径,即可得解.
,进而可求得外接球半径,即可得解.
取![]() 的中点
的中点![]() ,易知
,易知![]() 为
为![]() 的外心,取
的外心,取![]() 的中点
的中点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由正方体的性质可得![]() 平面
平面![]() ,
,
则三棱锥![]() 的外接球球心
的外接球球心![]() 在直线
在直线![]() 上,连接
上,连接![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
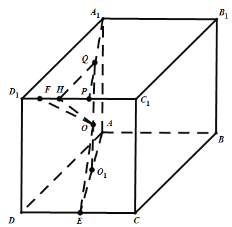
由中位线的性质可得![]() 且
且![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
若要使三棱锥![]() 的外接球的表面积最小,则要使其半径即
的外接球的表面积最小,则要使其半径即![]() 最小,
最小,
易知当![]() 即点
即点![]() 与
与![]() 重合时,
重合时,![]() 最小,
最小,
设![]() ,由题意
,由题意![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由![]() 可得
可得![]() ,化简可得
,化简可得![]() ,
,
此时,三棱锥![]() 的外接球的半径
的外接球的半径![]() 满足
满足![]() ,
,
所以三棱锥![]() 的外接球的表面积最小值
的外接球的表面积最小值![]() .
.
故选:C.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
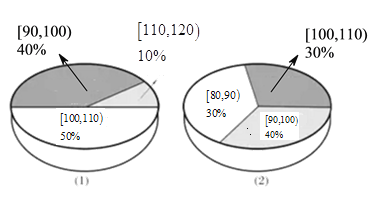
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的3月12日是植树节,某公司为了动员职工积极参加植树造林,在植树节期间开展植树有奖活动,设有甲、乙两个摸奖箱,每位植树者植树每满30棵获得一次甲箱内摸奖机会,植树每满50棵获得一次乙箱内摸奖机会,每箱内各有10个球(这些球除颜色外全相同),甲箱内有红、黄、黑三种颜色的球,其中![]() 个红球,
个红球,![]() 个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
(1)经统计,每人的植树棵数![]() 服从正态分布
服从正态分布![]() ,若其中有200位植树者参与了抽奖,请估计植树的棵数
,若其中有200位植树者参与了抽奖,请估计植树的棵数![]() 在区间
在区间![]() 内并中奖的人数(结果四舍五入取整数);
内并中奖的人数(结果四舍五入取整数);
附:若![]() ,则
,则![]() ,
,
![]() .
.
(2)若![]() ,某位植树者获得两次甲箱内摸奖机会,求中奖金额
,某位植树者获得两次甲箱内摸奖机会,求中奖金额![]() (单位:元)的分布列;
(单位:元)的分布列;
(3)某人植树100棵,有两种摸奖方法,
方法一:三次甲箱内摸奖机会;
方法二:两次乙箱内摸奖机会;
请问:这位植树者选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与OM垂直,垂足为P.
且与OM垂直,垂足为P.
(1)当![]() 时,求在直角坐标系下点
时,求在直角坐标系下点![]() 坐标和l的方程;
坐标和l的方程;
(2)当M在C上运动且P在线段OM上时,求点P在极坐标系下的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
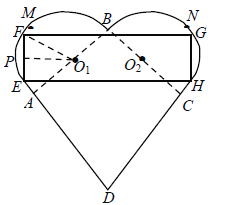
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() :
:![]() 的焦点
的焦点![]() ,且与拋物线
,且与拋物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)设点![]() 在笫一象限,过
在笫一象限,过![]() 作拋物线
作拋物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com