练习册

  • 练习册
  • 试题
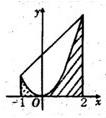    精英家教网 > 高中数学 > 题目详情
    函数y=（
    1
    2
    ）x在[1，2]上的值域为（　　）
    分析：利用指数函数的单调性，求出函数在[1，2]上的最大、最小值，即可得到函数在[1，2]上的值域．
    解答：解：∵
    1
    2
    ∈（0，1），
    ∴指数函数y=（
    1
    2
    ）x在[1，2]上为减函数，
    可得函数的最大值为f（1）=
    1
    2
    ，最小值为f（2）=
    1
    4
    ．
    因此，函数y=（
    1
    2
    ）x在[1，2]上的值域为[
    1
    4
    ，
    1
    2
    ]．
    故选：D
    点评：本题给出指数函数，求函数在给定区间上的值域．着重考查了指数函数的单调性和函数值域的求法等知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，设T是直线x=-1，x=2与函数y=x2的图象在x轴上方围成的直角梯形区域，S是T内函数y=x2图象下方的点构成的区域（图中阴影部分）．向T中随机投一点，则该点落入S中的概率为（　　）
    A、
    1
    5
    B、
    2
    5
    C、
    1
    3
    D、
    1
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知2x≤（
    1
    4
    ）x-3，求函数y=（
    1
    2
    ）x的值域．
    （2）函数y=
    ax+b
    1+x2
    是定义在（-1，1）上的奇函数，且f(
    1
    2
    )=
    2
    5
    ，求函数f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：f(x)=
    		1-a•3x
    在x∈（-∞，0]上有意义，命题q：函数y=lg（ax2-x+a）的定义域为R．如果p和q有且仅有一个正确，则a的取值范围
    （-∞，
    1
    2
    ]∪（1，+∞）
    （-∞，
    1
    2
    ]∪（1，+∞）
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北岳中高中一轮复习理科数学滚动测试三解析版 题型：解答题

    (12分)如图所示：图1是定义在R上的二次函数f(x)的部分图象，图2是函数g(x)＝loga(x＋b)的部分图象．

     

    (1)分别求出函数f(x)和g(x)的解析式；

    (2)如果函数y＝g(f(x))在区间[1，m)上单调递减，求m的取值范围．

     

    查看答案和解析>>

    同步练习册答案