
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
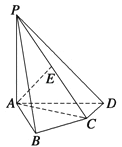
(1)求PB和平面PAD所成的角的大小;
(2)证明AE⊥平面PCD.
【答案】(1)45°;(2)见解析
【解析】
试题(1)先找出PB和平面PAD所成的角,再进行求解即可;
(2)可以利用线面垂直根据二面角的定义作角,再证明线面垂直.
(1)解:在四棱锥P﹣ABCD中,
因PA⊥底面ABCD,AB平面ABCD,
故PA⊥AB.
又AB⊥AD,PA∩AD=A,
从而AB⊥平面PAD,
故PB在平面PAD内的射影为PA,从而∠APB为PB和平面PAD所成的角.
在Rt△PAB中,AB=PA,故∠APB=45°.
所以PB和平面PAD所成的角的大小为45°.
(2)证明:在四棱锥P﹣ABCD中,
因为PA⊥底面ABCD,CD平面ABCD,
所以CD⊥PA.
因为CD⊥AC,PA∩AC=A,
所以CD⊥平面PAC.
又AE平面PAC,所以AE⊥CD.
由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
又PC∩CD=C,
所以AE⊥平面PCD.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.


查看答案和解析>>
科目:高中数学 来源: 题型:
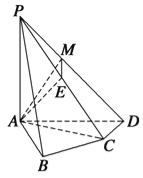
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
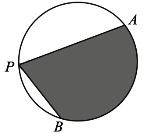
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△MBC中,MA是BC边上的高,MA=3,AC=4,将△MBC沿MA进行翻折,使得∠BAC=90°如图,再过点B作BD∥AC,连接AD,CD,MD且![]() ,∠CAD=30°.
,∠CAD=30°.
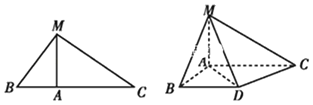
(1)求证:平面MCD⊥平面MAD;
(2)求点B到平面MAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
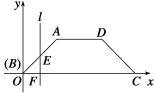
【题目】如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=1+ax,在(0,2]上f(x)≥0恒成立,q函数g(x)=ax+2lnx在其定义域上存在极值.
(1)若p为真命题,求实数a的取值范围;
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com