
定议在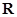 上的单调函数
上的单调函数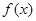 满足
满足 ,且对任意
,且对任意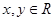 都有
都有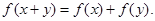
(1)求证: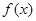 为奇函数;
为奇函数;
(2)若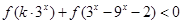 对任意
对任意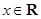 恒成立,求实数
恒成立,求实数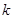 的取值范围.
的取值范围.
(1)详见解析:(2)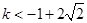 .
.
解析试题分析:(1)赋值法求解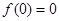 ,再寻找
,再寻找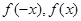 之间的关系;(2)先研究函数的单调性,再利用奇偶性化为
之间的关系;(2)先研究函数的单调性,再利用奇偶性化为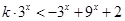 ,即
,即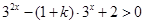 对任意的
对任意的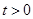 恒成立,再转化为二次函数知识求解.本题考查了恒成立问题以及化归与转化思想.
恒成立,再转化为二次函数知识求解.本题考查了恒成立问题以及化归与转化思想.
试题解析:(1)证明: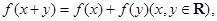 ①
①
令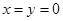 ,代入①式,得
,代入①式,得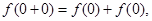 即
即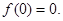
令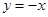 ,代入①式,得
,代入①式,得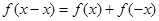 ,又
,又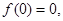
则有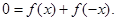 即
即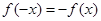 对任意
对任意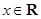 成立,
成立,
所以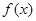 是奇函数. 4分
是奇函数. 4分
(2)解: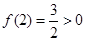 ,即
,即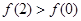 ,又
,又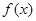 在
在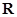 上是单调函数,
上是单调函数,
所以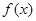 在
在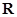 上是增函数.
上是增函数.
又由(1)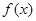 是奇函数.
是奇函数.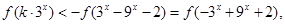
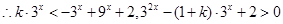 对任意
对任意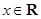 成立.
成立.
令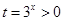 ,问题等价于
,问题等价于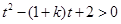 对任意
对任意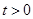 恒成立. 8分
恒成立. 8分
令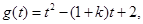 其对称轴
其对称轴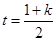 .
.
当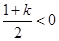 时,即
时,即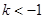 时,
时,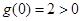 ,符合题意;
,符合题意;
当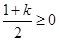 时,对任意
时,对任意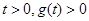 恒成立
恒成立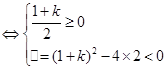
解得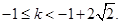 12分
12分
综上所述当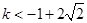 时,
时,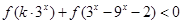 对任意
对任意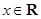 恒成立.
恒成立.
考点:1.函数奇偶性的证明;2.二次函数恒成立问题;3.化归与转化思想.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:解答题
已知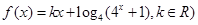 是偶函数.
是偶函数.
(1)求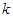 的值;
的值;
(2)证明:对任意实数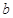 ,函数
,函数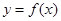 的图像与直线
的图像与直线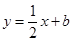 最多只有一个交点;
最多只有一个交点;
(3)设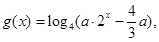 若函数
若函数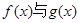 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一般情况下,大桥上的车流速度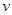 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到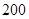 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当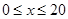 时,车流速度为
时,车流速度为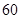 千米/小时.研究表明:当
千米/小时.研究表明:当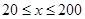 时,车流速度
时,车流速度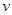 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)当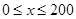 时,求函数
时,求函数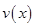 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)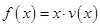 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数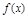 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若方程f(x)=0在[-1,1]上有实数根,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
工厂生产某种产品,次品率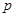 与日产量
与日产量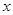 (万件)间的关系
(万件)间的关系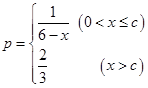 (
( 为常数,且
为常数,且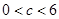 ),已知每生产一件合格产品盈利
),已知每生产一件合格产品盈利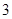 元,每出现一件次品亏损
元,每出现一件次品亏损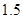 元.
元.
(1)将日盈利额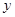 (万元)表示为日产量
(万元)表示为日产量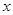 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式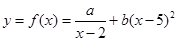 ,其中
,其中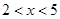 ,
, 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
(1)求 的解析式;
的解析式;
(2)若该商品的成本为2元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润
的值,使商场每日销售该商品所获得的利润 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数f(x)满足f (x+1)-f (x)=2x且f (0)=1.
⑴求f (x)的解析式;
⑵在区间[-1,1]上,y=f (x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数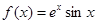 .
.
(Ⅰ)求函数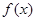 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的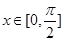 ,
,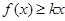 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在正实数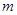 ,使得:当
,使得:当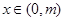 时,不等式
时,不等式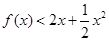 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为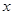 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为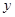 .
.
(Ⅰ)写出当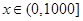 时,
时,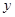 关于
关于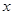 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于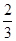 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com