
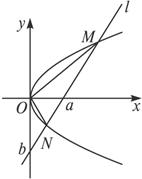
(1)写出直线l的截距式方程;
(2)证明![]() +
+![]() =
=![]() ;
;
(3)当a=2p时,求∠MON的大小.
剖析:易知直线l的方程为![]() +
+![]() =1,欲证
=1,欲证![]() +
+![]() =
=![]() ,即求
,即求![]() 的值,为此只需求直线l与抛物线y2=2px交点的纵坐标.由根与系数的关系易得y1+y2、y1y2的值,进而证得
的值,为此只需求直线l与抛物线y2=2px交点的纵坐标.由根与系数的关系易得y1+y2、y1y2的值,进而证得![]() +
+![]() =
=![]() .由
.由![]() ·
·![]() =0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
=0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
(1)解:直线l的截距式方程为![]() +
+![]() =1. ①
=1. ①
(2)证明:由①及y2=2px消去x可得by2+2pay-2pab=0. ②
点M、N的纵坐标y1、y2为②的两个根,故y1+y2=![]() ,y1y2=-2pa.
,y1y2=-2pa.
所以![]() +
+![]() =
=![]() =
=![]() =
=![]() .
.
(3)解:设直线OM、ON的斜率分别为k1、k2,
则k1=![]() ,k2=
,k2=![]() .
.
当a=2p时,由(2)知,y1y2=-2pa=-4p2,
由y12=2px1,y22=2px2,相乘得
(y1y2)2=4p2x1x2,
x1x2=![]() =
=![]() =4p2,因此k1k2=
=4p2,因此k1k2=![]() =
=![]() =-1.
=-1.
所以OM⊥ON,即∠MON=90°.
讲评:本题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力.


科目:高中数学 来源: 题型:
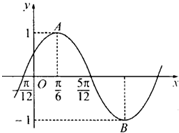 如图是函数y=sin(ωx+φ)的图象的一部分,A,B是图象上的一个最高点和一个最低点,O为坐标原点,则
如图是函数y=sin(ωx+φ)的图象的一部分,A,B是图象上的一个最高点和一个最低点,O为坐标原点,则| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
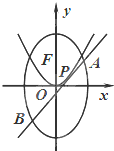 已知点是F抛物线C 1:x2=4y与椭圆C 2:
已知点是F抛物线C 1:x2=4y与椭圆C 2:| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
| 20 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
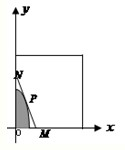 某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com