【答案】
分析:(1)根据当直线l过E
2的上顶点时,直线l的倾斜角为
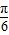
,且椭圆的离心率是
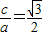
,建立方程,即可求得椭圆E
2的方程;
(2)当直线l垂直x轴时,易求得|AC|=|DB|.当直线l不垂直x轴时,设l:y=k(x-

),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系得出x
1+x
2=x
3+x
4从而有|AC|=|DB|.
(3)由(2)知,|AC|=|CD|+2,先分类讨论:当直线l垂直x轴时,不合要求;当直线l不垂直x轴时,设l:y=k(x-
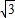
),由(2)知,x
1+x
2=x
3+x
4,x
1x
2,x
3x
4,利用弦长公式即可得关于k的方程,从而解决问题.
解答:解:(1)∵b=1,

,∴a=2,b=1,
因此椭圆E
2的方程为

x
2+y
2=1.
(2)当直线l垂直x轴时,易求得A(-

,-
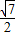
),C(-
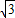
,-

),D(-

,

),B(-
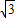
,
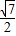
)
因此|AC|=|DB|.
当直线l不垂直x轴时,设l:y=k(x-

)
由
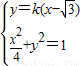
得(1+4k
2)x
2+8

k
2x+12k
2-4=0 ①,
由

得(1+4k
2)x
2+8
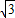
k
2x+12k
2-10=0 ②,
设A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),D(x
4,y
4),则x
3、x
4是方程①的解,
x
1、x
2是方程②的解.∵x
1+x
2=x
3+x
4=
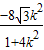
,
线段AB,CD的中点重合,∴|AC|=|DB|.
(3).由(2)知,|AC|=|CD|+2,
当直线l垂直x轴时,不合要求;
当直线l不垂直x轴时,设l:y=k(x-
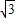
),由(2)知,
x
1+x
2=x
3+x
4=
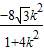
,x
1x
2=
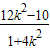
,
x
3x
4=

,|CD|=
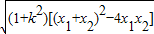
=

,
|AB|=
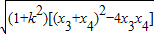
=
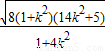
,
∴
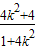
+2=

,
化简可得:8k
4-2k
2-1=(4k
2+1)(2k
2-1)=0,
∴k=

,
∴l:y=

(x+
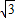
).
点评:本题考查椭圆与椭圆的标准方程,考查直线与椭圆的位置关系,正确运用韦达定理是关键.

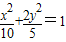 E2:
E2: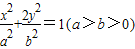 .E1与E2有相同的离心率,过点F(
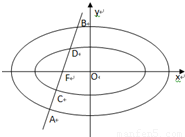
.E1与E2有相同的离心率,过点F(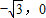 )的直线l与E1,E2依次交于A,C,D,B四点(如图).当直线l过E2的上顶点时,直线l的倾斜角为
)的直线l与E1,E2依次交于A,C,D,B四点(如图).当直线l过E2的上顶点时,直线l的倾斜角为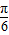 .
.
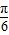 ,且椭圆的离心率是
,且椭圆的离心率是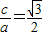 ,建立方程,即可求得椭圆E2的方程;
,建立方程,即可求得椭圆E2的方程; ),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系得出x1+x2=x3+x4从而有|AC|=|DB|.
),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系得出x1+x2=x3+x4从而有|AC|=|DB|.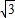 ),由(2)知,x1+x2=x3+x4,x1x2,x3x4,利用弦长公式即可得关于k的方程,从而解决问题.
),由(2)知,x1+x2=x3+x4,x1x2,x3x4,利用弦长公式即可得关于k的方程,从而解决问题. ,∴a=2,b=1,
,∴a=2,b=1, x2+y2=1.
x2+y2=1. ,-
,-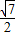 ),C(-
),C(-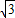 ,-
,- ),D(-
),D(- ,
, ),B(-
),B(-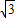 ,
,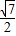 )
) )
)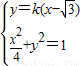
 k2x+12k2-4=0 ①,
k2x+12k2-4=0 ①,
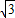 k2x+12k2-10=0 ②,
k2x+12k2-10=0 ②,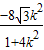 ,
,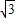 ),由(2)知,
),由(2)知,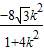 ,x1x2=
,x1x2=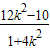 ,
, ,|CD|=
,|CD|=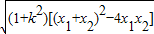 =
= ,
,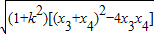 =
=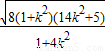 ,
,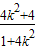 +2=
+2= ,
, ,
, (x+
(x+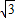 ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为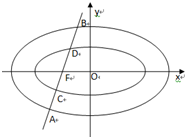 已知椭圆E1:
已知椭圆E1: ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.