
(2007
浙江,22)设 ,对任意实数t,记
,对任意实数t,记 .
.
(1)
求函数 的单调区间;
的单调区间;
(2)
求证:①当x>0时, 对任意正实数t成立;
对任意正实数t成立;
②
有且仅有一个正实数 ,使得
,使得 对任意正实数t成立.
对任意正实数t成立. |
解析: (1)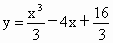 .由 .由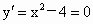 ,得x=±2. ,得x=±2.
因为当 x (-∞,-2)时, (-∞,-2)时, >0, >0,
当 x (-2,2)时, (-2,2)时,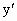 <0,当x <0,当x (2,+∞)时, (2,+∞)时, >0, >0,
故所求函数的单调递增区间是 (-∞,-2),(2,+∞),单调递减区间是(-2,2).(2)① 令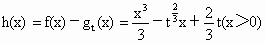 , ,
则  ,当t>0时,由 ,当t>0时,由 ,得 ,得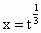 . .
当 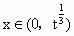 时, 时,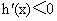 ,当 ,当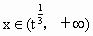 时,h(x)>0, 时,h(x)>0,
所以 h(x)在(0,+∞)内的最小值是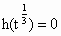 , ,
故当 x>0时, 对任意正实数t成立. 对任意正实数t成立.
② 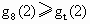 对任意正实数t成立,即存在正实数 对任意正实数t成立,即存在正实数 ,使得 ,使得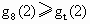 对任意正实数t成立.下面证明 对任意正实数t成立.下面证明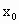 的唯一性:当 的唯一性:当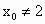 , , ,t=8时, ,t=8时,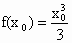 , , . .
由 ①得,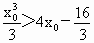 ,再取 ,再取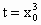 ,得 ,得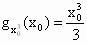 , ,
所以 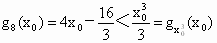 , ,
即  时,不满足 时,不满足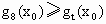 对任意t>0都成立. 对任意t>0都成立.
故有且仅有一个正实数  ,使得 ,使得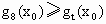 对任意正实数t成立. 对任意正实数t成立. |
|
剖析:本题主要考查函数的基本性质,导数的应用及不等式的证明等基本知识,以及综合运用所学知识分析和解决问题的能力. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com