
(1)求点C的轨迹方程;
(2)若![]() ,①试确定点F的坐标;②设P是点C的轨迹上的动点,猜想△PBF的周长最大时点P的位置,并证明你的猜想.
,①试确定点F的坐标;②设P是点C的轨迹上的动点,猜想△PBF的周长最大时点P的位置,并证明你的猜想.
解:(1)如图,设点C(x,y)(x≠0)、E(xE,0).F(xF,0),
由A、C、E三点共线,![]() ,
,
xE=![]() ,同理由B、C、F三点共线可得xF=
,同理由B、C、F三点共线可得xF=![]() .
.
∵![]() =4,
=4,
∴xE·xF=![]() ·
·![]() =4化简得C的轨迹方程为x2+4y2=4(x≠0).
=4化简得C的轨迹方程为x2+4y2=4(x≠0).
(2)若![]() ,①设F(xF,0),C(xc,yc),
,①设F(xF,0),C(xc,yc),
∴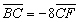
![]() (xc,yc+1)=-8(xF-xc,-yc),
(xc,yc+1)=-8(xF-xc,-yc),
∴xc=![]() xF,yc=
xF,yc=![]() ,代入x2+4y2=4得
,代入x2+4y2=4得
xF=±![]() ,
,
∴点F(±3,0),即为椭圆的焦点.
②猜想:取F(![]() ,0),设F1(-
,0),设F1(-![]() ,0)是左焦点,则当点P位于直线BF1与椭圆的交点处时,△PBE周长最大为8.证明如下:
,0)是左焦点,则当点P位于直线BF1与椭圆的交点处时,△PBE周长最大为8.证明如下:
∵|PF|+|PB|=4-|PF1|+|PB|≤4+|BF1|,
∴△PBF的周长≤4+|BF1|+|BF|=8.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com