
 在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.
在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.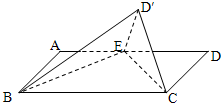 (1)证明:∵AD=2AB=2,E是AD的中点,
(1)证明:∵AD=2AB=2,E是AD的中点, ,
, ×1×1=
×1×1= ,∴V三棱锥B-D′EC=
,∴V三棱锥B-D′EC= ×
× ×
× =
= . …(9分)
. …(9分) ,
, ×
× ×1=
×1= ,∴V三棱锥E-D′BC=
,∴V三棱锥E-D′BC= ×
× ×h …(12分)
×h …(12分) .
. . …(14分)
. …(14分) ×
× ×
× =
= ,V三棱锥E-D′BC=
,V三棱锥E-D′BC= ×
× ×h,利用V三棱锥E-D′BC=V三棱锥B-D′EC,即可求得结论.
×h,利用V三棱锥E-D′BC=V三棱锥B-D′EC,即可求得结论.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
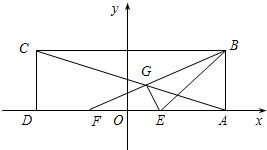 在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.
在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:查看答案和解析>>
科目:高中数学 来源: 题型:
 在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,
在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,查看答案和解析>>
科目:高中数学 来源: 题型:
 在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.
在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=3AD,E,F为AB的两个三等分点,AC,DF交于点G;
如图,在矩形ABCD中,已知AB=3AD,E,F为AB的两个三等分点,AC,DF交于点G;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com