
【题目】如图,直线![]() 与圆
与圆 ![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点.
两点.

(1)若直线![]() 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长![]()
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,判断
,判断![]() 是否为定值,并说明理由
是否为定值,并说明理由
(3)求![]() ,面积的最小值.
,面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由题意设直线![]() 由直线与圆相切可得
由直线与圆相切可得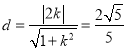 ,可得
,可得![]() ,故分两种情况可求得
,故分两种情况可求得![]() 。(2)(ⅰ)当直线
。(2)(ⅰ)当直线![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;(ⅱ)当
;(ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 将其代入圆的方程得
将其代入圆的方程得![]() ,根据斜率公式及根与系数的关系计算可得
,根据斜率公式及根与系数的关系计算可得![]() 。从而可得
。从而可得![]() 。(3)(ⅰ)当
。(3)(ⅰ)当![]() 斜率不存在或为
斜率不存在或为![]() 时,可得
时,可得![]() 。当
。当![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设直线
时,设直线![]() ,可求得
,可求得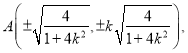 点B的坐标为
点B的坐标为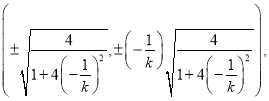
故可得![]()
![]() ,令
,令![]() ,则
,则![]()
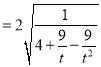 ,故当
,故当![]()
![]() 有最小值,且
有最小值,且 ![]() .
.
试题解析:
(1)由题意直线![]() 斜率存在,设直线
斜率存在,设直线![]()
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以
解得![]()
当![]() 时,由
时,由 解得
解得![]() ,所以
,所以![]()
当![]() 时,同理
时,同理![]()
所以![]() 。
。
(2)(ⅰ)当直线![]() 的斜率不存在时,得
的斜率不存在时,得![]() ;
;
(ⅱ)当![]() 的斜率存在时,设直线
的斜率存在时,设直线![]()
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以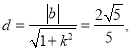
整理得所以![]() ①,
①,
由![]() 消去y整理得
消去y整理得![]() ,
,
由直线与圆相交得![]()
设![]()
则![]()
![]() ,②
,②
所以![]() ③,
③,
将①②代入③式得![]()
综上可得![]()
(3)由(2)知![]()
法一:(ⅰ)当![]() 斜率不存在或为
斜率不存在或为![]() 时,可得
时,可得![]() ,
,
(ⅱ)当![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设直线
时,设直线![]() ,
,
由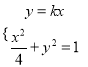 ,解得
,解得
所以点A的坐标为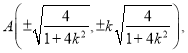
同理点B的坐标为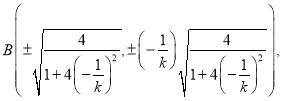
所以![]()
![]() ,
,
令![]() ,
,
所以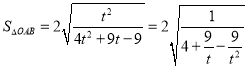 ,
,
故当![]()
![]() 有最小值,且
有最小值,且 ![]() .
.
综上可得![]() 面积的最小值为
面积的最小值为![]() 。
。
法二:记直线![]() 与圆
与圆![]() 的切点为
的切点为![]()
设![]()
所以![]() ,
,
则![]()
所以当![]() 时,
时, ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a5=15,数列{bn}满足b1=4,b4=20,且{bn﹣an}(n∈N+)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
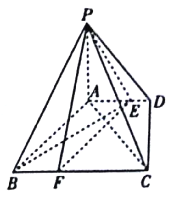
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的角A、B、C所对的边分别是a、b、c,设向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,边长c=2,角C=
,边长c=2,角C= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(2x+ ![]() )的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点(
)的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点( ![]() ,0)对称;
,0)对称;
②图象C关于直线x= ![]() 对称;
对称;
③由图象C向右平移 ![]() 个单位长度可以得到y=3sin2x的图象;
个单位长度可以得到y=3sin2x的图象;
④函数f(x)在区间(﹣ ![]() ,
, ![]() )内是减函数;
)内是减函数;
⑤函数|f(x)+1|的最小正周期为 ![]() .
.
其中正确的结论序号是 . (把你认为正确的结论序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com