
ЎѕМвДїЎїЎ¶ЦР»ЄИЛГс№ІєН№ъГс·ЁЧЬФтЎ·ЈЁТФПВјтіЖЎ¶Гс·ЁЧЬФтЎ·Ј©ЧФ2017Дк10ФВ1ИХЖрК©РР.ЧчОЄГс·ЁµдµДїЄЖЄЦ®ЧчЈ¬Ў¶Гс·ЁЧЬФтЎ·УлГїёцИЛµДТ»ЙъПўПўПа№Ш.ДіµШЗшОЄБЛµчСР±ѕµШЗшИЛГЗ¶ФёГ·ЁВЙµДБЛЅвЗйїцЈ¬Лж»ъійИЎ50ИЛЈ¬ЛыГЗµДДкБд¶јФЪЗшјд![]() ЙПЈ¬ДкБдµДЖµВК·ЦІјј°БЛЅвЎ¶Гс·ЁЧЬФтЎ·µДИлКэИзПВ±нЈє
ЙПЈ¬ДкБдµДЖµВК·ЦІјј°БЛЅвЎ¶Гс·ЁЧЬФтЎ·µДИлКэИзПВ±нЈє
ДкБд |
|
|
|
|
|
|
ЖµКэ | 5 | 5 | 10 | 15 | 5 | 10 |
БЛЅвЎ¶Гс·ЁЧЬФтЎ· | 1 | 2 | 8 | 12 | 4 | 5 |
ЈЁ1Ј©МоРґПВГж![]() БРБЄ±нЈ¬ІўЕР¶ПКЗ·сУР
БРБЄ±нЈ¬ІўЕР¶ПКЗ·сУР![]() µД°СОХИПОЄТФ45ЛкОЄ·ЦЅзµг¶ФБЛЅвЎ¶Гс·ЁЧЬФтЎ·ХюІЯУРІоТмЈ»
µД°СОХИПОЄТФ45ЛкОЄ·ЦЅзµг¶ФБЛЅвЎ¶Гс·ЁЧЬФтЎ·ХюІЯУРІоТмЈ»
ДкБдµНУЪ45ЛкµДИЛКэ | ДкБдІ»µНУЪ45ЛкµДИЛКэ | єПјЖ | |
БЛЅв |
|
| |
І»БЛЅв |
|
| |
єПјЖ |
ЈЁ2Ј©Иф¶ФДкБдФЪ![]() Ј¬
Ј¬![]() µД±»µчСРИЛЦРёчЛж»ъСЎИЎ2ИЛЅшРРЙоИлµчСРЈ¬јЗСЎЦРµД4ИЛЦРІ»БЛЅвЎ¶Гс·ЁЧЬФтЎ·µДИЛКэОЄ
µД±»µчСРИЛЦРёчЛж»ъСЎИЎ2ИЛЅшРРЙоИлµчСРЈ¬јЗСЎЦРµД4ИЛЦРІ»БЛЅвЎ¶Гс·ЁЧЬФтЎ·µДИЛКэОЄ![]() Ј¬ЗуЛж»ъ±дБїµД·ЦІјБРєНКэС§ЖЪНы.
Ј¬ЗуЛж»ъ±дБїµД·ЦІјБРєНКэС§ЖЪНы.
ІОїј№«КЅєНКэѕЭЈє
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
Ўѕґр°ёЎї(1)2ЎБ2БРБЄ±н
ДкБдµНУЪ45ЛкµДИЛКэ | ДкБдІ»µНУЪ45ЛкµДИЛКэ | єПјЖ | |
БЛЅв | a=3 | c=29 | 32 |
І»БЛЅв | b=7 | d=11 | 18 |
єПјЖ | 10 | 40 | 50 |
Г»УР99%µД°СОХИПОЄТФ45ЛкОЄ·ЦЅзµг¶ФБЛЅвЎ¶Гс·ЁЧЬФтЎ·ХюІЯУРІоТмЈ®
(2)XµД·ЦІјБРКЗ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() ;
;
ЎѕЅвОцЎї
(1)АыУГ±нёсКэѕЭЈ¬ёщѕЭБЄБР±нАыУГ№«КЅЗуЅвјґїЙЈ®
(2)НЁ№эXµДИЎЦµЈ¬ЗуіцёЕВКЈ¬µГµЅ·ЦІјБРЈ¬И»єуЗуЅвЖЪНыјґїЙЈ®
(1)2ЎБ2БРБЄ±н
ДкБдµНУЪ45ЛкµДИЛКэ | ДкБдІ»µНУЪ45ЛкµДИЛКэ | єПјЖ | |
БЛЅв | a=3 | c=29 | 32 |
І»БЛЅв | b=7 | d=11 | 18 |
єПјЖ | 10 | 40 | 50 |
![]() ,
,
ЛщТФГ»УР99%µД°СОХИПОЄТФ45ЛкОЄ·ЦЅзµг¶ФБЛЅвЎ¶Гс·ЁЧЬФтЎ·ХюІЯУРІоТмЈ®
(2)XЛщУРїЙДЬИЎЦµУР0Ј¬1Ј¬2Ј¬3Ј¬
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
ЛщТФXµД·ЦІјБРКЗ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ЛщТФXµДЖЪНыЦµКЗ![]() .
.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэh(x)ЈЅ(m2Ј5mЈ«1)xm+1ОЄГЭєЇКэЈ¬ЗТОЄЖжєЇКэЈ®
(I)ЗуmµДЦµЈ»
(II)ЗуєЇКэg(x)ЈЅh(x)Ј«![]() Ј¬xЎК
Ј¬xЎК![]() µДЦµУтЈ®
µДЦµУтЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»ёцХэ·ЅРО±»ЖК·ЦОЄ4ёцХэ·ЅРОЈ¬ЖК·ЦНјµД±ЯКэОЄ12.ИфТ»ёцХэ·ЅРО±»ЖК·ЦОЄ2005ёцН№¶а±ЯРОЈ¬КФЗуЖК·ЦНјЦР±ЯКэµДЧоґуЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙи![]() Ўў
Ўў![]() КЗБЅМхІ»Н¬µДЦ±ПЯЈ¬
КЗБЅМхІ»Н¬µДЦ±ПЯЈ¬![]() Ўў
Ўў![]() Ўў
Ўў![]() КЗИэёцІ»Н¬µДЖЅГжЈ¬Фт
КЗИэёцІ»Н¬µДЖЅГжЈ¬Фт![]() µДТ»ёцід·ЦМхјюКЗЈЁ Ј©
µДТ»ёцід·ЦМхјюКЗЈЁ Ј©
A.ґжФЪТ»МхЦ±ПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
B.ґжФЪТ»МхЦ±ПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
C.ґжФЪТ»ёцЖЅГж![]() Ј¬ВъЧг
Ј¬ВъЧг![]() Ј¬
Ј¬![]()
D.ґжФЪБЅМхТмГжЦ±ПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄaЈ¬bОЄХэКэЈ¬Ц±ПЯy=x©Ѓ2a+1УлЗъПЯy=ex+b©Ѓ1ПаЗРЈ¬Фт![]() µДЧоРЎЦµОЄЈЁЎЎЎЎЈ©
µДЧоРЎЦµОЄЈЁЎЎЎЎЈ©
A. 9 B. 7 C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪИэАвЦщ![]() ЦРЈ¬
ЦРЈ¬![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() ·Ц±рКЗ
·Ц±рКЗ![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() µДЦРµг.
µДЦРµг.
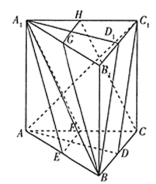
ЈЁ1Ј©ЗуЦ¤Јє![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() ЛДµг№ІГжЈ»
ЛДµг№ІГжЈ»
ЈЁ2Ј©ЗуЦ¤ЈєЖЅГж![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ3Ј©Иф![]() Ўў
Ўў![]() ·Ц±рОЄ
·Ц±рОЄ![]() Ўў
Ўў![]() µДЦРµгЈ¬ЗуЦ¤ЈєЖЅГж
µДЦРµгЈ¬ЗуЦ¤ЈєЖЅГж![]() ЖЅГж
ЖЅГж![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї2019Дк12ФВТФАґЈ¬єю±±ОдєєКР·ўПЦ¶аЖрІЎ¶ѕРФ·ОСЧІЎАэЈ¬ІўСёЛЩФЪИ«№ъ·¶О§ДЪїЄКјґ«ІҐЈ¬ЧЁјТЧйИПОЄЈ¬±ѕґОІЎ¶ѕРФ·ОСЧІЎАэµДІЎФМеіхІЅЕР¶ЁОЄРВРН№ЪЧґІЎ¶ѕЈ¬ёГІЎ¶ѕґжФЪИЛУлИЛЦ®јдµДґ«ИѕЈ¬їЙТФНЁ№эУл»јХЯµДГЬЗРЅУґҐЅшРРґ«Иѕ.ОТГЗ°СУл»јХЯУР№эГЬЗРЅУґҐµДИЛИєіЖОЄГЬЗРЅУґҐХЯЈ¬ГїО»ГЬЗРЅУґҐХЯ±»ёРИѕєујґ±»іЖОЄ»јХЯ.ТСЦЄГїО»ГЬЗРЅУґҐХЯФЪЅУґҐТ»ёц»јХЯєу±»ёРИѕµДёЕВКОЄ![]() Ј¬ДіО»»јХЯФЪёфАлЦ®З°Ј¬ГїМмУР
Ј¬ДіО»»јХЯФЪёфАлЦ®З°Ј¬ГїМмУР![]() О»ГЬЗРЅУґҐХЯЈ¬ЖдЦР±»ёРИѕµДИЛКэОЄ
О»ГЬЗРЅУґҐХЯЈ¬ЖдЦР±»ёРИѕµДИЛКэОЄ![]() Ј¬јЩЙиГїО»ГЬЗРЅУґҐХЯІ»ФЩЅУґҐЖдЛы»јХЯ.
Ј¬јЩЙиГїО»ГЬЗРЅУґҐХЯІ»ФЩЅУґҐЖдЛы»јХЯ.
ЈЁ1Ј©ЗуТ»МмДЪ±»ёРИѕИЛКэОЄ![]() µДёЕВК
µДёЕВК![]() Ул
Ул![]() Ўў
Ўў![]() µД№ШПµКЅєН
µД№ШПµКЅєН![]() µДКэС§ЖЪНыЈ»
µДКэС§ЖЪНыЈ»
ЈЁ2Ј©ёГІЎ¶ѕФЪЅшИлИЛМеєуУР14МмµДЗ±·ьЖЪЈ¬ФЪХв14МмµДЗ±·ьЖЪДЪ»јХЯОЮИОєОЦўЧґЈ¬ОЄІЎ¶ѕґ«ІҐµДЧојСК±јдЈ¬ЙиГїО»»јХЯФЪ±»ёРИѕєуµДµЪ¶юМмУЦУР![]() О»ГЬЗРЅУґҐХЯЈ¬ґУДіТ»Гы»јХЯ±»ёРИѕЈ¬°ґµЪ1МмЛгЖ𣬵Ъ
О»ГЬЗРЅУґҐХЯЈ¬ґУДіТ»Гы»јХЯ±»ёРИѕЈ¬°ґµЪ1МмЛгЖ𣬵Ъ![]() МмРВФц»јХЯµДКэС§ЖЪНыјЗОЄ
МмРВФц»јХЯµДКэС§ЖЪНыјЗОЄ![]() .
.
ЈЁiЈ©ЗуКэБР![]() µДНЁПʽЈ¬ІўЦ¤ГчКэБР
µДНЁПʽЈ¬ІўЦ¤ГчКэБР![]() ОЄµИ±ИКэБРЈ»
ОЄµИ±ИКэБРЈ»
ЈЁiiЈ©ИфґчїЪХЦДЬЅµµНГїО»ГЬЗРЅУґҐХЯ»јІЎёЕВКЈ¬ЅµµНєуµД»јІЎёЕВК![]() Ј¬µ±
Ј¬µ±![]() ИЎЧоґуЦµК±Ј¬јЖЛгґЛК±
ИЎЧоґуЦµК±Ј¬јЖЛгґЛК±![]() Лщ¶ФУ¦µД
Лщ¶ФУ¦µД![]() ЦµєНґЛК±
ЦµєНґЛК±![]() ¶ФУ¦µД
¶ФУ¦µД![]() ЦµЈ¬ёщѕЭјЖЛгЅб№ыЛµГчґчїЪХЦµД±ШТЄРФ.ЈЁИЎ
ЦµЈ¬ёщѕЭјЖЛгЅб№ыЛµГчґчїЪХЦµД±ШТЄРФ.ЈЁИЎ![]() Ј©
Ј©
ЈЁЅб№ы±ЈБфХыКэЈ¬ІОїјКэѕЭЈє![]() Ј©
Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј®
Ј®
ЈЁ1Ј©МЦВЫfЈЁxЈ©µДµҐµчРФЈ»
ЈЁ2Ј©ЗуєЇКэ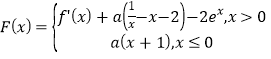 µДБгµгёцКэЈ®
µДБгµгёцКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЎчABCЦРЈ¬ДЪЅЗAЈ¬BЈ¬CµД¶Ф±Я·Ц±рОЄaЈ¬bЈ¬cЈ¬ТСЦЄ![]() .
.
(1)ЗуЅЗCµДЦµЈ»
(2)ИфcЈЅ2Ј¬ЗТЎчABCµДГж»эОЄ![]() Ј¬ЗуaЈ¬b.
Ј¬ЗуaЈ¬b.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com