
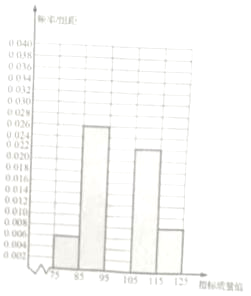
����Ŀ����ij��ҵ������ij�ֲ�Ʒ�г�ȡ100����������Щ��Ʒ��һ������ָ��ֵ���ɲ������õ�����Ƶ�ʷֲ�ֱ��ͼ
��1����ȫ�����Ƶ�ʷֲ�ֱ��ͼ������Ӱ��ʾ����
��2��ͳ�Ʒ����У�ͬһ�����ݳ��ø���������м�ֵ��Ϊ�������ݴ˹������ֲ�Ʒ����ָ��ֵ������̬�ֲ�Z���̣���2�������Ц̽���Ϊ����ƽ��ֵ![]() ����2����Ϊ��������s2��������ȡ�м�ֵ����
����2����Ϊ��������s2��������ȡ�м�ֵ����
�����ø���̬�ֲ�����Ӹó������IJ�Ʒ����ȡһ�����ò�ƷΪ�ϸ�Ʒ�ĸ��ʣ�
�ڸ���ҵÿ���������ֲ�Ʒ10���������һ���ϸ�Ʒ����10Ԫ������һ�����ϸ�Ʒ����20Ԫ�������ҵ���������Ƕ��٣�
�ο����ݣ�![]() ��5.1����Z��N���̣���2������P���̩��ң���+�ң���0.6826��P���̩�2�ң���+2�ң���0.9544��
��5.1����Z��N���̣���2������P���̩��ң���+�ң���0.6826��P���̩�2�ң���+2�ң���0.9544��
���𰸡���1������������2����0.9544����863200��
��������
��1����Ƶ�ʷֲ�ͼ���[95��105����Ƶ�ʣ��ɴ���������ȫƵ�ʷֲ�ֱ��ͼ��
��2���������ָ��ֵ������ƽ����������ָ��ֵ���������
���ɣ�2��֪Z��N��100��104�����Ӷ����P��79.6��Z��120.4����ע�������������ݣ�
�������ֲ�Ʒÿ������Ϊ�������E��X�����������EX��
��1����Ƶ�ʷֲ�ֱ��ͼ�ã�[95��105����Ƶ��Ϊ��1����0.006+0.026+0.022+0.008����10��0.038����ȫ�����Ƶ�ʷֲ�ֱ��ͼ������Ӱ��ʾ����

����ָ��ֵ������ƽ����Ϊ��
![]() ��80��0.06+90��0.26+100��0.38+110��0.22+120��0.08��100��
��80��0.06+90��0.26+100��0.38+110��0.22+120��0.08��100��
����ָ��ֵ����������Ϊ
S2������20��2��0.06+����10��2��0.26+0��0.38+102��0.22+202��0.08��104��
��2�����ɣ�1��֪Z��N��100��104�����Ӷ�P��79.6��Z��120.4����P��100��2��10.2��Z��100+2��10.2����0.9544��
������֪һ����Ʒ������ָ��ֵλ�����䣨79.6��120.4���ĸ���Ϊ0.9544��
����ҵ����������EX��100000[0.9544��10����1��0.9544����20]��863200��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ԲC�IJ�������Ϊ![]() Ϊ����
Ϊ����![]() ������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ֱ�ߵļ����귽��Ϊ
������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ֱ�ߵļ����귽��Ϊ![]() ����Բ��C��ֱ��l�ϣ�
����Բ��C��ֱ��l�ϣ�
![]() ��
��![]() ��ֱ��l��ֱ�����귽�̼�ԲC�ļ����귽�̣�
��ֱ��l��ֱ�����귽�̼�ԲC�ļ����귽�̣�
![]() ��
��![]() ��
��![]() ��ֱ��l��һ�㣬
��ֱ��l��һ�㣬![]() ��ԲC��һ�㣬��
��ԲC��һ�㣬��![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У���֪
�У���֪![]() ƽ��
ƽ��![]() ��
��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��![]() ��
��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() .
.
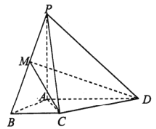
(��)֤����![]() ƽ��
ƽ��![]() ��
��
(��)��![]() ��
��![]() ���е㣬������
���е㣬������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ������������ԭ��![]() �����Ķ��᳤Ϊ
�����Ķ��᳤Ϊ![]() ��һ������Ϊ
��һ������Ϊ![]() ��һ������
��һ������![]() ����
����![]() ������
������![]() ��ֱ������Բ�ཻ������
��ֱ������Բ�ཻ������![]() .
.![]() .
.
��1������Բ�ķ��̼�������.
��2�������![]() Ϊֱ����Բ��ԭ�㣬��ֱ��
Ϊֱ����Բ��ԭ�㣬��ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ����
����![]() ��
�� ![]() ���㣬��Բ����ֱ��
���㣬��Բ����ֱ��![]() �ϣ�
�ϣ�
��1����Բ![]() �ı����̣�
�ı����̣�
��2����Բ![]() ��һ��
��һ��![]() ���������ֱ����
���������ֱ����![]() ����
����![]() ʱ�����ı���
ʱ�����ı���![]() �������
�������
��3����ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ���㣬
���㣬 ![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����ex��![]() ��������ֵ�㣮
��������ֵ�㣮
��1����ʵ��a��ȡֵ��Χ��
��2��������f��x����������ֵ��ֱ�Ϊx1��x2����֤��x1+x2��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵���һ����ӻ���ʹ��ʱ�䣬�о���Ա�Ըÿ���ӻ���������Ӧ�IJ��ԣ����õ�������ͳ������ͼ��ʾ��

���Բ�ͬ����������������ӻ��Ĺ�����Ը�������飬�õ����������±���ʾ��
Ը��������ӻ� | ��Ը��������ӻ� | �ܼ� | |
40������ | 800 | 1000 | |
40������ | 600 | ||
�ܼ� | 1200 |
��1������ͼ�е����ݣ��Թ��Ƹÿ���ӻ���ƽ��ʹ��ʱ�䣻
��2�����ݱ������ݣ��ж��Ƿ���99.9%�İ�����Ϊ��Ը���ÿ���ӻ����롰��������䡱�йأ�
��3�������յ��ӻ���ʹ��ʱ����зֲ��������ʹ��ʱ����![]() ��
��![]() �ĵ��ӻ��г�ȡ5̨���ٴ���5̨�������ȡ2̨���������⣬��ȡ��2̨���ӻ���ʹ��ʱ�䶼��
�ĵ��ӻ��г�ȡ5̨���ٴ���5̨�������ȡ2̨���������⣬��ȡ��2̨���ӻ���ʹ��ʱ�䶼��![]() �ڵĸ��ʣ�
�ڵĸ��ʣ�
���� | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г��о���ԱΪ���˽��ҵ�����ļ�˾ǰ�ڵľ�Ӫ״�����Ըù�˾2018�����������µ����������ͳ�ƣ������ݵõ������ݻ�������Ӧ������ͼ����ͼ��ʾ
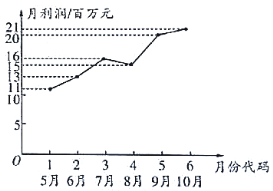
��1��������ͼ���Կ������������Իع�ģ�����������![]() ����λ������Ԫ�����·ݴ���
����λ������Ԫ�����·ݴ���![]() ֮��Ĺ�ϵ����
֮��Ĺ�ϵ����![]() ����
����![]() �����Իع鷽�̣���Ԥ��ù�˾2019��3�·ݵ�����
�����Իع鷽�̣���Ԥ��ù�˾2019��3�·ݵ�����
��2����˾��������һ���Ʒ����Ҫ�ɹ�һ�����Ͳ��ϣ�����![]() ��
��![]() �����ͺŵ����Ͳ��Ͽɹ�ѡ���涨ÿ�����Ͳ�������ʹ��
�����ͺŵ����Ͳ��Ͽɹ�ѡ���涨ÿ�����Ͳ�������ʹ��![]() ���£����²��ϵIJ��ȶ��Իᵼ�²�����������ͬ���ֶ�
���£����²��ϵIJ��ȶ��Իᵼ�²�����������ͬ���ֶ�![]() ��
��![]() �����ͺŵ����Ͳ��϶�Ӧ�IJ�Ʒ��
�����ͺŵ����Ͳ��϶�Ӧ�IJ�Ʒ��![]() �����п�ѧģ����ԣ��õ��������Ͳ���ʹ��������Ƶ��ͳ�����±���
�����п�ѧģ����ԣ��õ��������Ͳ���ʹ��������Ƶ��ͳ�����±���
ʹ������ �������� |
|
|
|
| �ܼ� |
|
|
|
|
|
|
|
|
|
|
|
|
������Ǽ�˾�ĸ����ˣ����ѡ��ɹ��Ŀ����Ͳ��ϣ�
�ο����ݣ�![]() ��
��![]() .�ο���ʽ���ع�ֱ�߷���Ϊ
.�ο���ʽ���ع�ֱ�߷���Ϊ![]() ������
������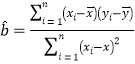
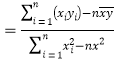 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ף����ڣ�ij��ѧ��ί��֯������������������л���֪ʶ�������Ӳμӿ��Ե�ѧ���г��60��������ɼ�(�ɼ���Ϊ����)�ֳ�[40��50)��[50��60)������[90��100)���飬��������ͼ��ʾ�IJ���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�Σ��ش��������⣺
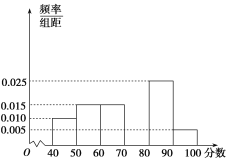
(1)��������Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
(2)������ο��Եļ�����(60�ּ�����Ϊ����)��ƽ���֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com