过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
A.x+y-2=0
B.y-1=0
C.x-y=0
D.x+3y-4=0
【答案】
分析:由扇形的面积公式可知,劣弧

所的扇形的面积

=2α,则S
2=4π-2α(∠AOB=α)要求面积差的最大值,即求α的最小值,根据直线与圆相交的性质可知,只要当OP⊥AB时,α最小,可求
解答:
解:设过点P(1,1)的直线与圆分别交于点A,B,且圆被AB所分的两部分的面积分别为S
1,S
2且S
1≤S
2劣弧

所对的圆心角∠AOB=α,则

=2α,S
2=4π-2α(0<α≤π)
∴S
△AOB+S
2-(S
1-S
△AOB)=4π-4α+
要求面积差的最大值,即求α的最小值,根据直线与圆相交的性质可知,只要当OP⊥AB时,α最小
此时K
AB=-1,直线AB的方程为y-1=-(x-1)即x+y-2=0
故选A
解:要使直线将圆形区域分成两部分的面积之差最大,必须使过点P的圆的弦长达到最小,所以需该直线与直线OP垂直即可.
又已知点P(1,1),则K
OP=1,
故所求直线的斜率为-1.又所求直线过点P(1,1),
由点斜式得,所求直线的方程为y-1=-(x-1),即.x+y-2=0
故选A
点评:本题主要考查了直线与圆相交性质的应用,解题的关键是根据扇形的面积公式把所要求解的两面积表示出来

 所的扇形的面积
所的扇形的面积 =2α,则S2=4π-2α(∠AOB=α)要求面积差的最大值,即求α的最小值,根据直线与圆相交的性质可知,只要当OP⊥AB时,α最小,可求
=2α,则S2=4π-2α(∠AOB=α)要求面积差的最大值,即求α的最小值,根据直线与圆相交的性质可知,只要当OP⊥AB时,α最小,可求 解:设过点P(1,1)的直线与圆分别交于点A,B,且圆被AB所分的两部分的面积分别为S1,S2且S1≤S2
解:设过点P(1,1)的直线与圆分别交于点A,B,且圆被AB所分的两部分的面积分别为S1,S2且S1≤S2 所对的圆心角∠AOB=α,则
所对的圆心角∠AOB=α,则 =2α,S2=4π-2α(0<α≤π)
=2α,S2=4π-2α(0<α≤π)


 椭圆E:
椭圆E: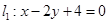 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
. 平行的直线方程;
平行的直线方程; 垂直的直线方程.
垂直的直线方程.![]() 与椭圆交于A,B两点,
与椭圆交于A,B两点,![]() 的面积为4,
的面积为4,![]() 的周长为
的周长为![]()