
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() 为
为![]() 的两个三等分点.
的两个三等分点.
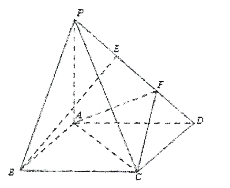
(1)求证![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)连结BD,AC相交于O,证明BE∥OF,即可证明BE∥平面ACF;(2)过A作AH⊥PC于H,利用面面垂直的性质证明AH⊥平面PCD,从而证明AH⊥CD,然后利用线面垂直的性质证明PC⊥CD.
(Ⅰ)连接BD、AC,两线交于O,
∴O是BD的中点(平行四边形对角线互相平分),
∵F是DE的中点(由三等分点得到),
∴OF是△DEB的中位线,∴BE∥OF,
∵OF面ACF,BE面ACF,
∴BE平行平面ACF.
(Ⅱ)过A作AH⊥PC于H,∵平面PAC⊥平面PCD,
∴AH⊥平面PCD,∵CD平面PCD,∴AH⊥CD,
∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.又∵PA∩AH=A,∴CD⊥平面PAC,
∵PC平面PAC,
∴PC⊥CD.


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为![]() 的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
(1)求抛物线C的标准方程;
(2)设点P为抛物线C上异于A,B的点,直线PA与PB分别交抛物线C的准线于E,G两点,x轴与准线的交点为H,求证:HGHE为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
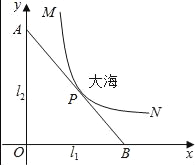
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中
(1)在等差数列![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
(2)已知等比数列![]() 为递增数列,且公比为
为递增数列,且公比为![]() ,若
,若![]() ,则当且仅当
,则当且仅当![]() ;
;
(3)若数列![]() 为递增数列,则
为递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
(4)已知数列![]() 满足
满足![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]()
(5)若![]() 是等比数列
是等比数列![]() 的前
的前![]() 项的和,且
项的和,且![]() ;(其中
;(其中![]() 、
、![]() 是非零常数,
是非零常数,![]() ),则A+B为零.
),则A+B为零.
其中正确命题是_________(只需写出序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】梯形![]() 顶点
顶点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]() 米.
米.
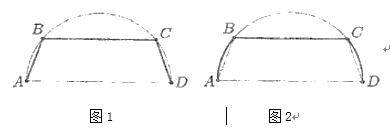
(1)如图1,若电热丝由![]() 这三部分组成,在
这三部分组成,在![]() 上每米可辐射1单位热量,在
上每米可辐射1单位热量,在![]() 上每米可辐射2单位热量,请设计
上每米可辐射2单位热量,请设计![]() 的长度,使得电热丝的总热量最大,并求总热量的最大值;
的长度,使得电热丝的总热量最大,并求总热量的最大值;
(2)如图2,若电热丝由弧![]() 和弦
和弦![]() 这三部分组成,在弧
这三部分组成,在弧![]() 上每米可辐射1单位热量,在弦
上每米可辐射1单位热量,在弦![]() 上每米可辐射2单位热量,请设计
上每米可辐射2单位热量,请设计![]() 的长度,使得电热丝辐射的总热量最大.
的长度,使得电热丝辐射的总热量最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
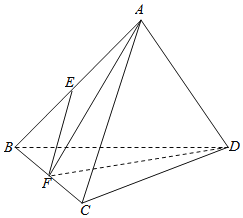
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:

(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(ⅰ)若日需求量为15个,求![]() ;
;
(ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: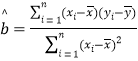
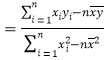 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com