
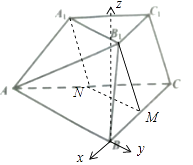
����Ŀ����ͼ��������̨ABC��A1B1C1�У�ƽ�������A1 �� B1 �� ��CC1��ƽ�����ƽ���������̨�����ཻ������Χ��һ���ı��Σ�
������ͼ�л�������ı��Σ���ָ���Ǻ����ı��Σ�����˵������������˵���ı��ε���״����
������AB=8��BC=2B1C1=6��AB��BC��BB1=CC1 �� ƽ��BB1C1C��ƽ��ABC�������B1��AB��C����60�㣬��ֱ��AB1��ƽ������ɽǵ�����ֵ��
���𰸡��⣺����Χ�ɵ��ı�����ͼ��ʾ������ƽ���ı��Σ�����AB��BC��ƽ��BB1C1C��ƽ��ABC��
��ƽ��BB1C1C��ƽ��ABC=BC��AB��ƽ��ABC
��AB��ƽ��BB1C1C��
��AB��BB1 �� ��B1BC�Ƕ����B1��AB��C��ƽ��ǣ�
���B1BC=60�㣬
��BC��ABΪx��y�ᣬBΪԭ�㽨����ͼֱ������ϵB��xyz��
����֪CC1�Φ���B1M=����ƽ��BB1C1C��֪B1M��CC1 ��
����̨������ʣ�BC��B1C1 ��
��MCC1B1��ƽ���ı��Σ�
��MC=B1C1=3��M��BC���е㣬
��BB1=CC1 �� ��B1��ƽ��ABC�ľ��룬h= ![]() ��
��
ͬ��N��AC���е㣬
A��0����8��0����B��0��0��0����B1���� ![]() ��0��
��0�� ![]() ����M����3��0��0����
����M����3��0��0����
�� ![]() =��
=�� ![]() ��0��
��0�� ![]() ����
���� ![]() =��0����4��0����
=��0����4��0���� ![]() =����
=���� ![]() ��8��
��8�� ![]() ����
����
��ƽ����ķ�����Ϊ ![]() =��x��y��z������
=��x��y��z������ 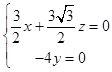
��һ���������� ![]() =��
=�� ![]() ��0����1����
��0����1����
��ֱ��AB1��ƽ������ɽ�Ϊ�ȣ���sin��=|  |=
|= ![]() ��
��
��ֱ��AB1��ƽ������ɽǵ�����ֵΪ ![]() ��
��
������������Χ�ɵ��ı�����ͼ��ʾ������ƽ���ı��Σ�������BC��ABΪx��y�ᣬBΪԭ�㽨����ͼֱ������ϵB��xyz�����ƽ����ķ����������������ļнǹ�ʽ��������ֱ��AB1��ƽ������ɽǵ�����ֵ��
�����㾫�����������⣬������Ҫ�˽�ƽ��Ļ������ʼ�����(���һ��ֱ���ϵ�������һ��ƽ���ڣ���ô����ֱ���ڴ�ƽ����;������һ��ֱ���ϵ����㣬����ֻ��һ��ƽ��;����������غϵ�ƽ����һ�������㣬��ô��������ֻ��һ�����õ�Ĺ���ֱ��)����Ҫ���տռ�ǵ�����ֱ�����ɵĽ�(��֪![]() Ϊ������ֱ�ߣ�A��C��B��D�ֱ���
Ϊ������ֱ�ߣ�A��C��B��D�ֱ���![]() �ϵ��������㣬
�ϵ��������㣬![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ����
����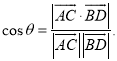 )�����֪ʶ���Ǵ���Ĺؼ���
)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵΪ�˽�����ij���ŶԱ���ҵְ���ķ���������������50��ְ����������50��ְ���Ըò��ŵ����֣�����Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������Ϊ![]()

��1����Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2�����Ƹ���ҵ��ְ���Ըò������ֲ�����80�ĸ��ʣ�
��3����������![]() ���ܷ�ְ���У������ȡ2�ˣ����2�����ֶ���
���ܷ�ְ���У������ȡ2�ˣ����2�����ֶ���![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ʯ��ׯ��ij��������˾�ҵ���һ������Ա�Ĺ������ù�˾������������нн�귽������������н100Ԫ��ÿ����һ������1Ԫ���ҷ�������н140Ԫ��ÿ��ǰ55��û�н���������55���IJ���ÿ������12Ԫ��
������ֱ�����ס�������н�귽������нy����λ��Ԫ�����ͻ�����n�ĺ�����ϵʽ��
�����ݸù�˾��������Ա100������ͼ�¼����������Ա����ƽ�����͵���������������������100���е�������ָ��������ͼ��ʾ��ֱ��ͼ�����е�ij���������ָ���ڣ�![]() ��
��![]() ]��n��1��2��3��4��5��ʱ����ƽ��������Ϊ50��2n��������Ƶ����Ϊ���ʣ��ش��������⣺
]��n��1��2��3��4��5��ʱ����ƽ��������Ϊ50��2n��������Ƶ����Ϊ���ʣ��ش��������⣺

�ٸ����������ݣ���ÿ������Ա����нΪX����λ��Ԫ�����Էֱ�����ס������ַ�������нX�ķֲ��У���ѧ���������
�ڽ�Ϣ��е����ݣ�����ͳ��ѧ��˼�룬����С����������ѡ������н�귽���ȽϺ��ʣ���˵��������ɡ�
���ο����ݣ�0��62��0��36��1��42��1��9 6��2��6 2��6��76��3��42��1 1��56��3��62��12��96��4��62��21��16��15��62��243��36��20��42��416��16��44��42��1971��36��
���𰸡������������ĺ�����ϵʽΪ�� ![]() ���ҷ����ĺ�����ϵʽΪ��
���ҷ����ĺ�����ϵʽΪ��![]() �������ټ��������ڼ�����.
�������ټ��������ڼ�����.
��������
������������ɵü���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ�� ![]() �� �ҷ���������Ա��н
�� �ҷ���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() .
.
�����������������X�ķֲ��У��ݴ˼���ɵ�![]() ��
��![]() ��
��![]() .
.
�ڴ�һ�������ϵļ����֪��![]() ԶС��
ԶС��![]() ���������չ������벨����Խ�С������С��Ӧѡ�����.
���������չ������벨����Խ�С������С��Ӧѡ�����.
�𰸶��������ϵļ��������Կ�����![]() ������С��Ӧѡ���ҷ���.
������С��Ӧѡ���ҷ���.
������������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ�� ![]() ��
��
�ҷ���������Ա��н![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]()
������������֪������100���У��ù�˾����Ա��ƽ�����͵����������±���
���� | 52 | 54 | 56 | 58 | 60 |
Ƶ�� | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
����![]()
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
����![]()
![]()
�ڴ�һ�������ϵļ����֪����Ȼ![]() ��������������
��������������![]() ԶС��
ԶС��![]() ���������չ������벨����Խ�С������С��Ӧѡ�����.
���������չ������벨����Խ�С������С��Ӧѡ�����.
�𰸶��������ϵļ��������Կ�����![]() ���������չ�������С���ҷ����չ�������������С��Ӧѡ���ҷ���.
���������չ�������С���ҷ����չ�������������С��Ӧѡ���ҷ���.
���㾦��
������Ҫ����Ƶ�ʷֲ�ֱ��ͼ����ѧ�����뷽��ĺ�����ʵ��Ӧ�õ�֪ʶ�����ڿ���ѧ����ת�������ͼ����������.
�����͡������
��������
20
����Ŀ����֪��ԲC��![]() ��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ
��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ![]() ��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��������ԲC�ķ��̣�
������֪��A����ԲC��������Բ�����һ�㣬�ӳ�ֱ��AF1��AF2�ֱ�����Բ���ڵ�B��D����ֱ��BD��б��Ϊk1��ֱ��OA��б��Ϊk2����֤��k1��k2���ڶ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x��y����Լ������  ����z=y��axȡ�����ֵ�����ŽⲻΨһ����ʵ��a��ֵΪ�� ��
����z=y��axȡ�����ֵ�����ŽⲻΨһ����ʵ��a��ֵΪ�� ��
A.![]() ��1
��1
B.2�� ![]()
C.2��1
D.2��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ������ȤС��Ϊ�о���ѧ�ɼ��Ƿ����Ա��йأ���ͳ�Ʊ�У�����꼶ÿ��ѧ��һѧ����ѧ�ɼ�ƽ����(���ðٷ���)����ƽ������40�����µ�ѧ����������300����Ů��200�����ֲ��÷ֲ�����ķ��������г�ȡ��100��ѧ�������Ա��Ϊ���飬��������ѧ���ɼ���Ϊ6�飬�õ�������ʾƵ���ֲ�����

��1�������С�Ů�����Ե�ƽ����(ͬһ�������ø��������е�ֵ������)���Ӽ�����������ѧ�ɼ����Ա��Ƿ��йأ�
��2���涨80������Ϊ�ŷ�(��80��)�����������֪��������2��2�����������ж��Ƿ���90%���ϵİ�����Ϊ����ѧ�ɼ����Ա��йء���

��������ʽ��
P(K2��k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ο��Թ���10��ѡ���⣬ÿ��ѡ���ⶼ��4��ѡ���������ֻ��һ������ȷ�ģ����ֱ��涨����ÿ��ֻѡһ��ѡ���Ե�5�֣�����������������ij������ȷ����7����Ĵ�����ȷ�ģ��������У���һ���ⶼ���ж�����ѡ���Ǵ���ģ���һ��������ж�һ��ѡ���Ǵ���ģ�����һ��������������ֻ���Ҳ£�������ÿ�����
����50�ֵĸ��ʣ�
�������÷���![]() ����ѧ��������С����ʾ����ȷ��0.01k^s*5#u��
����ѧ��������С����ʾ����ȷ��0.01k^s*5#u��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ֱ������ϵ��ԭ���غϣ�������x����������غϣ�ԲC�ļ����귽���Ǧ�=asin�ȣ�ֱ��l�IJ��������� 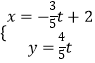 ��tΪ������
��t������
��1����a=2��ֱ��l��x��Ľ�����M��N��ԲC��һ���㣬��|MN|�����ֵ��
��2��ֱ��l��ԲC�صõ��ҳ�����ԲC�İ뾶�� ![]() ������a��ֵ��
������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���������ijɼ�������Ķ���֮��Ĺ�ϵ��ij�о����������ȡ��60����������ͨ���ʾ����飬�õ��������ݣ�
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

���������ݣ�����õ�K2�Ĺ۲�ֵk��9.643�������ٽ�ֵ��������˵����ȷ����(����)
A. û�г����������Ϊ�����Ķ����������ijɼ������й�
B. ��0.5%�İ�����Ϊ�����Ķ����������ijɼ������й�
C. ��99.9%�İ�����Ϊ�����Ķ����������ijɼ������й�
D. ��99.5%�İ�����Ϊ�����Ķ����������ijɼ������й�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=![]() x2+alnx��
x2+alnx��
��1����a=��1������f��x���ļ�ֵ����ָ������ֵ���Ǽ�Сֵ��
��2����a=1������f��x����[1��e]�ϵ���ֵ��
��3����a=1����֤��������[1��+�����ϣ�����f��x����ͼ����g��x��=![]() x3��ͼ���·���
x3��ͼ���·���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com