
用数学归纳法证明“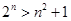 对于
对于 的自然数
的自然数 都成立”时,第一步证明中的起始值
都成立”时,第一步证明中的起始值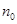 应取( )
应取( )
A.2 B.3 C.5 D.6
C
【解析】
试题分析:根据数学归纳法的步骤,首先要验证当n取第一个值时命题成立;
结合本题,要验证n=1时,左=21=2,右=12+1=2,2n>n2+1不成立,
n=2时,左=22=4,右=22+1=5,2n>n2+1不成立,
n=3时,左=23=8,右=32+1=10,2n>n2+1不成立,
n=4时,左=24=16,右=42+1=17,2n>n2+1不成立,
n=5时,左=25=32,右=52+1=26,2n>n2+1成立,
因为n>5成立,所以2n>n2+1恒成立.
故选C.
考点:本题主要考查数学归纳法的概念及方法步骤。
点评:解此类问题时,注意n的取值范围。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com