
【题目】已知菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于一点
相交于一点![]() ,
, ![]() ,将
,将![]() 沿着
沿着![]() 折起得
折起得![]() ,连接
,连接![]() .
.
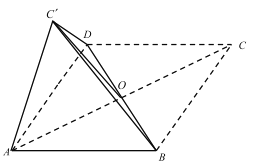
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在平面
在平面![]() 上的投影恰好是
上的投影恰好是![]() 的重心,求直线
的重心,求直线![]() 与底面
与底面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)只需证明![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
即可得平面平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 在平面
在平面![]() 上的投影为
上的投影为![]() ,即
,即![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,并过
,并过![]() 作
作![]() 于点
于点![]() ,即可证得
,即可证得![]() 是
是![]() 与底面
与底面![]() 所成的角,进而求解.
所成的角,进而求解.
试题解析:
(1)因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)方法一:设![]() 在平面
在平面![]() 上的投影为
上的投影为![]() ,即
,即![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
连结![]() ,并过
,并过![]() 作
作![]() 于点
于点![]() ,
,
因为![]() 平面
平面![]() ,即
,即![]() ,且有
,且有![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() ,
,
又因为![]() ,且
,且![]() ,故
,故![]() 平面
平面![]() ,
,
从而知![]() 是
是![]() 与底面
与底面![]() 所成的角,
所成的角,
设![]() ,则在
,则在![]() 中有
中有![]() ,
, ![]() ,所以
,所以![]() ,故
,故![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() ,即
,即![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

(2)方法二:如图建系![]() ,
,
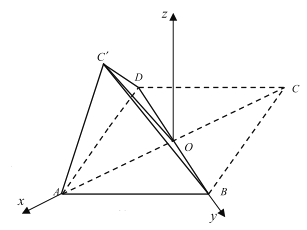
令![]() ,则知
,则知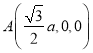 ,
, ![]() ,
, ![]() ,
, 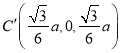 ,
,
即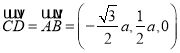 ,平面
,平面![]() 的法向量为
的法向量为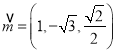 ,
,
故![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜爱打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜爱打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附: 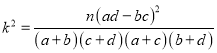
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的![]() ,得曲线C.
,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l: ![]() 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴求函数![]() 的单调区间;
的单调区间;
⑵如果对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶设函数![]() ,
, ![]() .过点
.过点![]() 作函数
作函数![]() 的图象
的图象
的所有切线,令各切点的横坐标构成数列![]() ,求数列
,求数列![]() 的所有项之和
的所有项之和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
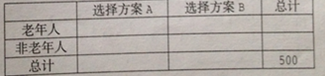
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选处建设方案A和B向社会公开征集意见,有关部分用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:
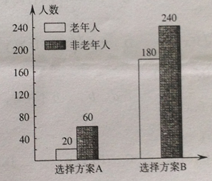
(1)根据已知条件完成下面![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过![]() 的前提下认为是否选择方案A和年龄段有关?
的前提下认为是否选择方案A和年龄段有关?
(2)根据(1)的结论,能否提出一个更高的调查方法,使得调查结果更具代表性,说明理由.
附:

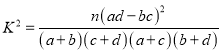
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com