
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
【答案】(1) 不变化;(2)![]() ;(3)先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小
;(3)先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小
【解析】
(1)按甲在先,乙次之,丙最后的顺序派人,任务能被完成的概率为![]()
![]() .
.
若甲在先,丙次之,乙最后的顺序派人,任务能被完成的概率为![]()
![]() ,
,
发现任务能完成的概率是一样.
同理可以验证,不论如何改变三个人被派出的先后顺序,任务能被完成的概率不发生变化.
(2)由题意得![]() 可能取值为
可能取值为![]()
∴![]() ,
,
∴其分布列为:
|
|
|
|
|
|
|
|
![]() .
.
(3)![]() ,
,![]()
∴要使所需派出的人员数目的均值(数字期望)达到最小,
则只能先派甲、乙中的一人.
∴若先派甲,再派乙![]() ;
;
若先派乙,再派甲,最后派丙, 则![]() ,
,
![]() ,
,
∴先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
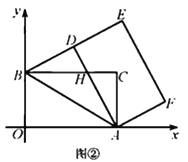
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() .
.

(1)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .
.
①求证![]() ;②求点
;②求点![]() 的坐标.
的坐标.
(3)记![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 的面积,求
的面积,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商家通过市场调研,发现某商品的销售价格y(元/件)和销售量x(件)有关,其关系可用图中的折线段![]() 表示(不包含端点A).
表示(不包含端点A).

(1)把y表示成x的函数;
(2)若该商品进货价格为12元/件,则商家卖出多少件时可以获得最大利润?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)讨论函数![]() 在定义域内极值点的个数;
在定义域内极值点的个数;
(3)设直线![]() 为函数
为函数![]() 的图象上一点
的图象上一点![]() 处的切线,证明:在区间
处的切线,证明:在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,![]() ·
·![]() =0,|
=0,|![]() |=12,|
|=12,|![]() |=15,l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点.
|=15,l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点.
(1)求![]() ·
·![]() 的值;
的值;
(2)判断![]() ·
·![]() 的值是否为一个常数,并说明理由.
的值是否为一个常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、国、美、丽”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计,恰好第三次就停止的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
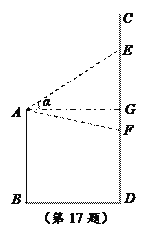
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com