
科目:高中数学 来源:2008年普通高等学校招生全国统一考试(上海卷)、数学 题型:044
已知z是实系数方程x2+2bx+c=0的虚根,记它在直角坐标平面上的对应点为Pz(Rez,Imz).
(1)若(b,c)在直线2x+y=0上,求证:Pz在圆C1:(x-1)2+y2=1上;
(2)给定圆C:(x-m)2+y2=r2(m、r∈R,r>0),则存在唯一的线段s满足:①若Pz在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则Pz在圆C上.写出线段s的表达式,并说明理由;
(3)由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写下表(表中s1是(1)中圆C1的对应线段).

查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如表:
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.406 5)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ( )
A.1.2 B.1.3
C.1.4 D.1.5
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如表:
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.406 5)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ( )
A.1.2 B.1.3
C.1.4 D.1.5
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)和g(x)分别由下表给出定义:
| x | 1 | 2 | 3 |
| f(x) | 2 | ________ | 3 |
| x | 1 | 2 | 3 |
| g(x) | 3 | ________ | 1 |
若方程f(g(x))=g(f(x))的解恰有2个,请在表中横线上填上合适的数.
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江虎林高中高二下学期期中理科数学试卷(解析版) 题型:解答题
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
|
零件的个数x(个) |
2 |
3 |
4 |
5 |
|
加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
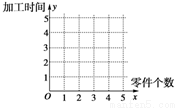
(2)求出y关于x的线性回归方程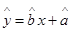 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注: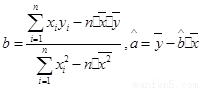 )
)
【解析】第一问中利用数据描绘出散点图即可
第二问中,由表中数据得 =52.5,
=52.5, 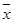 =3.5,
=3.5, =3.5,
=3.5,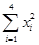 =54,∴
=54,∴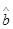 =0.7,
=0.7,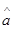 =1.05得到回归方程。
=1.05得到回归方程。
第三问中,将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时)得到结论。
(1)散点图如下图.
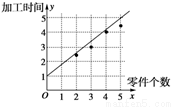 ………………4分
………………4分
(2)由表中数据得 =52.5,
=52.5, 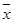 =3.5,
=3.5, =3.5,
=3.5,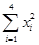 =54,
=54,
∴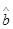 =…=0.7,
=…=0.7,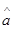 =…=1.05.
=…=1.05.
∴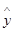 =0.7x+1.05.回归直线如图中所示.………………8分
=0.7x+1.05.回归直线如图中所示.………………8分
(3)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时),
∴预测加工10个零件需要8.05小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com