
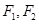 为双曲线
为双曲线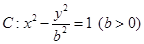 的左、右焦点,过
的左、右焦点,过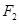 作垂直于
作垂直于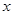 轴的直线,在
轴的直线,在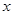 轴上方交双曲线于点
轴上方交双曲线于点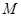 ,且
,且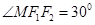 ,圆
,圆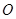 的方程为
的方程为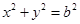 .
. 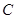 的方程;
的方程;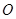 上任意一点
上任意一点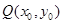 作切线
作切线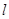 交双曲线
交双曲线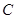 于
于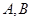 两个不同点,
两个不同点,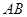 中点为
中点为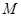 ,
,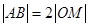 ;
;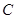 上一点
上一点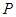 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是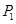 和
和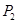 ,求
,求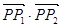 的值
的值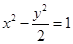 ;(2)见解析;(3)
;(2)见解析;(3)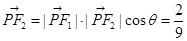
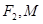 的坐标分别为
的坐标分别为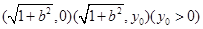 ----------------1分
----------------1分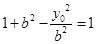 ,即
,即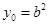 ,所以
,所以 ------2分
------2分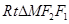
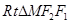 中,
中, ,
,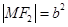 ,所以
,所以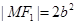 -------3分
-------3分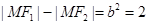
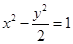 -------------------4分
-------------------4分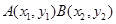 ,切线
,切线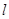 的方程为:
的方程为: 
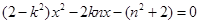
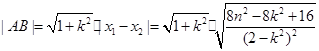 -------------------6分
-------------------6分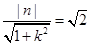 ,代入上式,得
,代入上式,得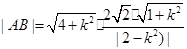 -----------7分
-----------7分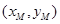 ,则
,则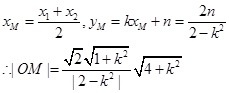
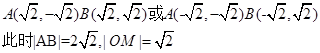 ,
,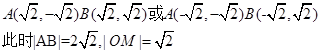
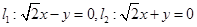 ------11分
------11分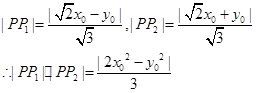 --------------13分
--------------13分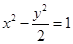 上,所以
上,所以
 -------------------14分
-------------------14分 -------------15分
-------------15分

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源:不详 题型:单选题
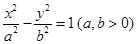 右支上一点,
右支上一点,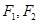 为双曲线的左、右焦点,O为坐标原点,若
为双曲线的左、右焦点,O为坐标原点,若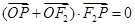 ,且
,且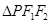 的面积为
的面积为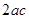 (
(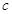 为双曲线的半焦距),则双曲线的离心率为( )
为双曲线的半焦距),则双曲线的离心率为( )A.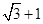 | B.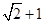 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com