
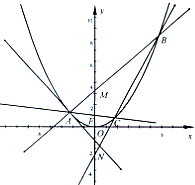
 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.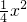 ,∴
,∴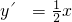 ,∴直线l的斜率k1=
,∴直线l的斜率k1=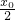
 ,∴直线AB的方程为y-y0=-
,∴直线AB的方程为y-y0=- (x-x0)
(x-x0) x2+
x2+ x-2-y0=0
x-2-y0=0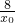 ,∴x1=-x0-
,∴x1=-x0-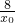
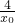
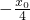 -
-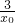 ,∴直线BC的方程为y-y2=(
,∴直线BC的方程为y-y2=(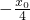 -
-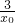 )(x-x2)
)(x-x2)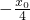 -
-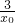 )(-x2)+y2,代入x2=-
)(-x2)+y2,代入x2=-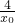 ,y2=
,y2=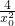 ,化简得y=-1-
,化简得y=-1-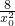
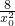 ),∴|MN|=y0+2+1+
),∴|MN|=y0+2+1+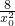 =
=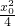 +
+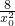 3≥3+2
3≥3+2 当且仅当x04=32时等号成立,
当且仅当x04=32时等号成立, .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
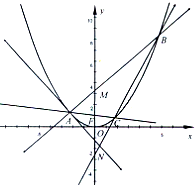 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.查看答案和解析>>
科目:高中数学 来源: 题型:
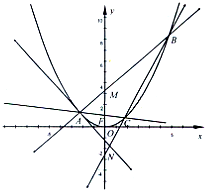 (2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
(2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴一中高三(上)10月月考数学试卷(文科)(解析版) 题型:填空题
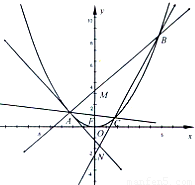
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴一中高三(上)10月月考数学试卷(文科)(解析版) 题型:填空题
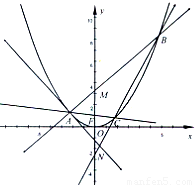
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com