
【题目】在矩形![]() 中,
中, ![]() 动点
动点![]() 在以点
在以点![]() 为圆心且与
为圆心且与![]() 相切的圆上,若
相切的圆上,若![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】如图:以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,
则A(0,0),B(1,0),D(0,2),C(1,2),
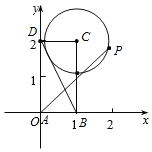
∵动点P在以点C为圆心且与BD相切的圆上,
设圆的半径为r,
∵BC=2,CD=1,
∴BD=![]() =
=![]()
∴![]() BCCD=
BCCD=![]() BDr,
BDr,
∴r=![]() ,
,
∴圆的方程为(x﹣1)2+(y﹣2)2=![]() ,
,
设点P的坐标为(![]() cosθ+1,
cosθ+1, ![]() sinθ+2),
sinθ+2),
∵![]() ,
,
∴(![]() cosθ+1,
cosθ+1, ![]() sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
∴![]() cosθ+1=λ,
cosθ+1=λ, ![]() sinθ+2=2μ,
sinθ+2=2μ,
∴λ+μ=![]() cosθ+
cosθ+![]() sinθ+2=sin(θ+φ)+2,其中tanφ=2,
sinθ+2=sin(θ+φ)+2,其中tanφ=2,
∵﹣1≤sin(θ+φ)≤1,
∴1≤λ+μ≤3,
故λ+μ的最大值为3,
故选:A


科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() 所得到如图所示的频率分布直方图.
所得到如图所示的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知左、右焦点分别为![]() 的椭圆
的椭圆![]() 与直线
与直线![]() 相交于
相交于![]() 两点,使得四边形
两点,使得四边形![]() 为面积等于
为面积等于![]() 的矩形.
的矩形.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 上一动点
上一动点![]() (不在
(不在![]() 轴上)作圆
轴上)作圆![]() 的两条切线
的两条切线![]() ,切点分别为
,切点分别为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 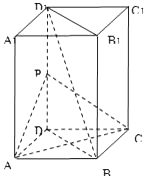
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1B1;
(3)求CP与平面BDD1B1所成的角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,分别求a和c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com