
(本题满分15分)已知集合M={1,2,3,4,5}, .
.
(1)用列举法表示集合
 ;
;
(2)设N是M的非空真子集,且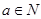 时,有
时,有 ,试写出所有集合N;
,试写出所有集合N;
(3)已知M的非空子集个数为31个,依次记为 ,分别求出它们各自的元素之和,结果依次记为
,分别求出它们各自的元素之和,结果依次记为 ,试计算:
,试计算: 的值.
的值.
(1)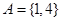 ;(2)单元子集
;(2)单元子集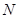 是
是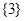 ,两个元素的子集
,两个元素的子集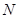 有
有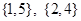
集合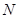 还有:
还有: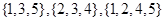 .
.
(3)在所有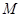 的真子集中,每个元素出现的次数均为
的真子集中,每个元素出现的次数均为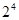
解析试题分析:(1)要注意集合A中的元素是M中不属于L的元素.显然是L相对于M的补集.
(2)N是M的非空真子集,然后从真子集当中选出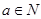 时,有
时,有 即可.据此可找出满足条件的N有:
即可.据此可找出满足条件的N有: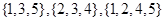
(3) 因为在所有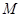 的真子集中,每个元素出现的次数均为
的真子集中,每个元素出现的次数均为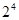 ,
,
所以所有集合中元素的和为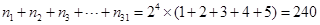 .
.
(1)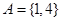 ……
……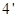
(2)单元子集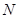 是
是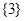 ,两个元素的子集
,两个元素的子集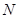 有
有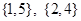 ……
……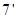
集合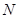 还有:
还有: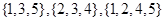 . ……
. ……
(3)在所有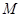 的真子集中,每个元素出现的次数均为
的真子集中,每个元素出现的次数均为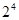
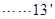
故 ……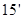 .
.
考点:集合的补运算,集合的元素的性质.
点评:本小题第(1)问实质是考查集合的补集的定义,第(2)问关键是搞清楚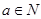 时,有
时,有 ,这个条件.第(3)知道如果集合M中有n个元素,则其非空真子集的个数为
,这个条件.第(3)知道如果集合M中有n个元素,则其非空真子集的个数为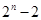 .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com