sin12°sin87°+sin78°cos87°= .
【答案】
分析:根据互余的两角的诱导公式,可得sin78°=cos12°,结合两角差的余弦公式将原式化成cos(12°-87°)=cos(-75°)=cos75°.再根据75°=45°+30°,用两角和的余弦公式展开并代入45°、30°的正弦、余弦之值,可得cos75°的值,从而得到原式的值.
解答:解:∵12°+78°=90°,∴sin78°=cos12°
因此,sin12°sin87°+sin78°cos87°
=sin12°sin87°+cos12°cos87°=cos(12°-87°)=cos(-75°)=cos75°
∵75°=45°+30°
∴cos75°=cos45°cos30°-sin45°sin30°=
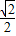
×
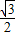
-
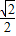
×

=
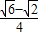
综上所述,可得sin12°sin87°+sin78°cos87°=

故答案为:
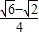 点评:
点评:本题给出三角函数式,要我们化简并求出它的值.着重考查了三角函数的诱导公式、两角和与差的余弦公式和特殊角的三角函数值等知识,属于基础题.

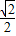 ×
×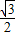 -
-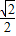 ×
× =
=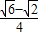

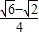


 阅读快车系列答案
阅读快车系列答案