数列{an}中,a1=1,且an+1=Sn(n≥1,n∈N*),数列{bn}是等差数列,其公差d>0,b1=1,且b3、b7+2、3b9成等比数列.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设数列{cn}满足cn=anbn,求{cn}的前n项和Tn.
【答案】
分析:(Ⅰ)由a
n+1=S
n,根据
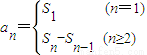
求得数列{a
n}通项公式,数列{b
n}是等差数列,其公差d>0,b
1=1,且b
3、b
7+2、3b
9成等比数列,求出数列{b
n}的公差,可求得数列{b
n}的通项公式;
(Ⅱ)把(Ⅰ)求得的结果代入c
n=a
nb
n,利用错位相减法求得{c
n}的前n项和T
n.
解答:解:(I)由已知有S
n+1-S
n=S
n,即S
n+1=2S
n(n∈N
*),
∴{S
n}是以S
1=a
1=1为首项,2为公比的等比数列.
∴S
n=2
n-1.
由
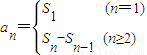
得

∵b
3,b
7+2,3b
9成等比数列,
∴(b
7+2)
2=b
3•3b
9,即(1+6d+2)
2=(1+2d)•3(1+8d),
解得d=1或d=
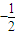
(舍),
∴b
n=1+(n-1)×1=n.
(II)T
n=a
1b
1+a
2b
2++a
nb
n=1×1+2×2
+3×2
1++n×2
n-2,
设T=2×2
+3×2
1++n×2
n-2,
∴2T=2×2
1+3×2
2++n×2
n-1,
相减得-T=2+2
1+2
2++2
n-2-n•2
n-1=

=(1-n)•2
n-1,
即T=(n-1)•2
n-1,
∴T
n=1+(n-1)•2
n-1(n∈N*).
点评:考查等差数列求通项公式,及利用
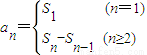
求得数列{a
n}通项公式的方法,体现分类讨论的思想方法,属中档题.

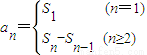 求得数列{an}通项公式,数列{bn}是等差数列,其公差d>0,b1=1,且b3、b7+2、3b9成等比数列,求出数列{bn}的公差,可求得数列{bn}的通项公式;
求得数列{an}通项公式,数列{bn}是等差数列,其公差d>0,b1=1,且b3、b7+2、3b9成等比数列,求出数列{bn}的公差,可求得数列{bn}的通项公式;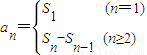 得
得
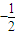 (舍),
(舍), =(1-n)•2n-1,
=(1-n)•2n-1,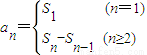 求得数列{an}通项公式的方法,体现分类讨论的思想方法,属中档题.
求得数列{an}通项公式的方法,体现分类讨论的思想方法,属中档题. 

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案