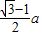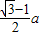在△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,以BD为棱折成直二面角A-BD-C,P是AB上的一点,若二面角P-CD-B为60°,则AP= .
【答案】
分析:由已知中△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,以BD为棱折成直二面角A-BD-C,P是AB上的一点,若二面角P-CD-B为60°,我们易得∴∠PAB即二面角P-CD-B的平面角,解三角形PAD,即可求出AP的长.
解答:解:∵在△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,
∴△ABC为等腰直角三角形,
则翻折后CD⊥平面ABD
则CD⊥AD,CD⊥PD
∴∠PAB即二面角P-CD-B的平面角等60°,
∴在△PAD中,AD=
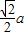
,∠A=45°,∠APD=105°
由正弦定理易得AP=
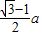
故答案为:
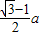 点评:
点评:本题考查的知识是二面角的平面角及求法,其中根据∴PAB即二面角P-CD-B的平面角等60°,将问题转化为解三角形问题是解答本题的关键.

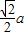 ,∠A=45°,∠APD=105°
,∠A=45°,∠APD=105°