
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
(1)求三棱锥C-A1B1C1![]() 的体积V;
的体积V;
(2)求直线BD1与平面ADB1所成角的正![]() 弦值;
弦值;
(3)若棱AA1上存在一点P,使得![]() =λ
=λ![]() ,当二面
,当二面![]() 角A-B1C1-P的大小为30
角A-B1C1-P的大小为30![]() °时,求实数λ的值.
°时,求实数λ的值.
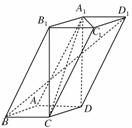
解:(1)在Rt△A1AD中,∠A1AD=90°,A1A=2,AD=1,
∴A1D=![]() .
.
注意到点C到面A1B1C1的距离即为四棱柱ABCD-A1B1C1D1的高A1D的长,
所以V=![]() ×
×![]() ×A1B1×B1C1×A1D=
×A1B1×B1C1×A1D=![]() .
.
(2)以点D为坐标原点,建立如图空间直角坐标系O-xyz,

则D(0,0,0),A(1,0,0),B(1,1,0),A1(0,0,![]() ),
),
B1(0,1,![]() ),D1(-1,0,
),D1(-1,0,![]() ),C1(-1,1,
),C1(-1,1,![]() ),
),
∴![]() =(-2,-1,
=(-2,-1,![]() ),
),![]() =(1,0,0),
=(1,0,0),![]() =(0,1,
=(0,1,![]() ),
),
设平面ADB1的法向量m=(x,y,z),
由 得平面ADB1的一个法向量为:
得平面ADB1的一个法向量为:
m=(0,-![]() ,1),
,1),
记直线BD1与平面ADB1所成的角为α,
则sin α=|![]() |=
|=![]() ,
,
所以直线BD1与平面ADB1所成角的正弦值为![]() .
.
(3)∵![]() =λ
=λ![]() ,∴P(
,∴P(![]() ,0,
,0,![]() ).
).
又![]() =(-1,0,
=(-1,0,![]() 0),
0),![]() =(
=(![]() ,-1,-
,-1,-![]() ),
),
设平面B1C1P的法向量n=(a,b,c),
由 得平面B1C1P的一个法向量为
得平面B1C1P的一个法向量为
n=(0,-![]() ,1),
,1),
则cos 30°=![]() =
= ,
,
注意到λ>0,解得λ=2为所求.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
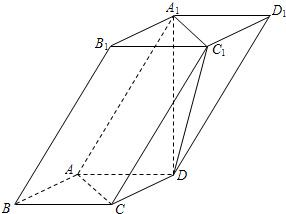 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:
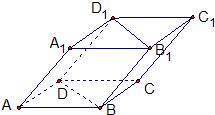 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是查看答案和解析>>
科目:高中数学 来源: 题型:
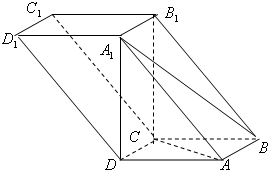 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,| AP |
| PA1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
| ||
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com