
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x ![]() 使不等式2f(x)≥g(x)成立,求实数a的取值范围.
使不等式2f(x)≥g(x)成立,求实数a的取值范围.
【答案】
(1)解:f′(x)=lnx+1,令f′(x)=0得x= ![]() ,
,
当x∈(0, ![]() )时,f′(x)<0,f(x)单调递减,
)时,f′(x)<0,f(x)单调递减,
当x∈( ![]() ,+∞)时,f′(x)>0,f(x)单调递增.
,+∞)时,f′(x)>0,f(x)单调递增.
①当0<t<t+2≤ ![]() 时,t无解;
时,t无解;
②当0<t< ![]() <t+2时,即0<t<
<t+2时,即0<t< ![]() 时,
时, ![]() =﹣
=﹣ ![]() ;
;
③当 ![]() ≤t<t+2时,即t≥
≤t<t+2时,即t≥ ![]() 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt;
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt;
∴f(x)min=  .
.
(2)解:x ![]() 时,
时,
2f(x)≥g(x)即2xlnx≥﹣x2+ax﹣3,亦即2lnx≥﹣x+a﹣ ![]() ,可化为2lnx+x+
,可化为2lnx+x+ ![]() ≥a,
≥a,
令h(x)=2lnx+x+ ![]() ,则问题等价于h(x)max≥a,
,则问题等价于h(x)max≥a,
h′(x)= ![]() +1﹣
+1﹣ ![]() =
= ![]() ,
,
当x∈[ ![]() ,1)时,h′(x)<0,h(x)递减;当x∈(1,e]时,h′(x)>0,h(x)递增;
,1)时,h′(x)<0,h(x)递减;当x∈(1,e]时,h′(x)>0,h(x)递增;
又h( ![]() )=2ln
)=2ln ![]() +
+ ![]() +3e=3e+
+3e=3e+ ![]() ﹣2,h(e)=2lne+e+
﹣2,h(e)=2lne+e+ ![]() =e+
=e+ ![]() +2,
+2,
而h(e)﹣h( ![]() )=﹣2e+
)=﹣2e+ ![]() +4<0,所以h(e)<h(
+4<0,所以h(e)<h( ![]() ),
),
故x ![]() 时,h(x)max=h(
时,h(x)max=h( ![]() )=3e+
)=3e+ ![]() ﹣2,
﹣2,
所以实数a的取值范围是:a≤3e+ ![]() ﹣2.
﹣2.
【解析】(1)对函数求导,根据导函数与0的关系写出函数的单调性和区间,讨论所给的区间和求出的单调区间之间的关系,在不同条件下做出函数的最值;(2)2f(x)≥g(x)可化为2lnx+x+ ![]() ≥a,令h(x)=2lnx+x+
≥a,令h(x)=2lnx+x+ ![]() ,则问题等价于h(x)max≥a,利用导数可求得x
,则问题等价于h(x)max≥a,利用导数可求得x ![]() 时h(x)max;
时h(x)max;
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】淘宝网卖家在某商品的所有买家中,随机选择男、女买家各50位进行调查,他们的评分等级如下表:

(1)从评分等级为(4,5]的人中随机选取2人,求恰有1人是男性的概率.
(2)现规定评分等级在[0,3]为不满意该商品,在(3,5]为满意该商品.完成下列2×2列联表,并帮助卖家判断能否在犯错误的概率不超过0.05的前提下认为是否满意该商品与性别有关.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始________h后,两车的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() =1(a>b>0)过点A
=1(a>b>0)过点A![]() ,离心率为
,离心率为![]() ,点F1,F2分别为其左、右焦点.
,点F1,F2分别为其左、右焦点.
(1)求椭圆E的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点P,Q,且![]() ?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.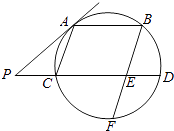
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2),M(1,0),![]() =(3λ,4λ)(λ≠0),
=(3λ,4λ)(λ≠0),![]() =-4
=-4![]() ,若抛物线y2=ax经过A和B两点,则a的值为( )
,若抛物线y2=ax经过A和B两点,则a的值为( )
A. 2 B. -2
C. -4 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com