
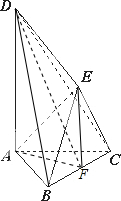
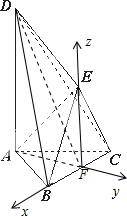
 如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2
如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2| 3 |
| BF |
| BD |
| 3 |
| 3 |
| 3 |
| DE |
| 3 |
| 3 |
| BE |
| 3 |
| AD2+AB2 |
| BF |
| BD |
| 1 |
| 4 |
| 3 |
| 3 |
| 3 |
 .
.| DE |
| 3 |
| 3 |
| BE |
| 3 |
| m |
|
| 3 |
| m |
| 3 |
| n |
| m |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 5 |


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
 如图所示,△ABC和△A'B'C'是在各边的
如图所示,△ABC和△A'B'C'是在各边的| 1 |
| 3 |
| a |
| 3 |
| GH |
| EA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.
如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第4章 平面向量):4.1 向量的有关概念(解析版) 题型:解答题
 处相交的两个正三角形,△ABC的边长为a,图中列出了长度均为
处相交的两个正三角形,△ABC的边长为a,图中列出了长度均为 的若干个向量,则
的若干个向量,则 相等的向量是 ;
相等的向量是 ; 平行的向量是 .
平行的向量是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com