练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    棱长为1的的正方体ABCD－A1B1C1D1中，求证：平面A1BD∥平面CB1D1．

    答案：
    解析：

    　　解析：过a和直线b上任意一点P作一平面γ和平面β交于，∵α∥β，∴a∥，∵，，，∴，∵，，b∥β，

    　　∴α∥β；8．∵A1B∥D1C，∴A1B∥平面CD1B1，同理BD∥平面CD1B1，

    　　∵A1B面A1BD，BD面A1BD，∴面A1BD∥面CD1B1．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和O2的表面积之和的最小值为（　　）
    A、(6-3
    		3
    )π
    B、(8-4
    		3
    )π
    C、(6+3
    		3
    )π
    D、(8+4
    		3
    )π

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－2)　2009－2010学年　第39期　总第195期 北师大课标 题型：044

    某种游戏中，黑、黄两个“电子狗”从棱长为1的正方体ABCD－A1B1C1D1的顶点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．黑“电子狗”爬行的路线是AA1——A1D1——…，黄“电子狗”爬行的路线是AB——BB1——…，它们都遵循如下规则：所爬行的第i＋2段与第i段所在的直线必须是异面直线(其中i是正整数)．设黑“电子狗”爬完2009段，黄“电子狗”爬完2008段后各自停留在正方体的某个顶点处，求这时黑、黄两个“电子狗”之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和O2的表面积之和的最小值为


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式

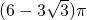
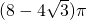
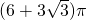
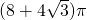
    查看答案和解析>>

    科目：高中数学 来源：2011年河北省石家庄市高考数学二模试卷（理科）（解析版） 题型：选择题

    两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和O2的表面积之和的最小值为（ ）
    A．
    B．
    C．
    D．

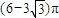
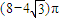
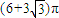
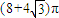
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （04年广东卷）在棱长为1的正方体上，分别过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的凸多面体的体积是

    (A)                   (B)                    (C)                   (D)

    查看答案和解析>>

    同步练习册答案