
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点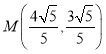 在椭圆C上,延长
在椭圆C上,延长![]() 交椭圆于N点.
交椭圆于N点.
(1)求椭圆C的方程;
(2)P,Q为椭圆上的点,记线段MN,PQ的中点分别为A,B(A,B异于原点O),且直线AB过原点O,求![]() 面积的最大值.
面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
其中正确结论的序号是( )
A.②④⑤B.①②④⑤C.①③④D.②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这第一产品期间第![]() 天的利润
天的利润 (单位:万元,
(单位:万元,![]() ),记第
),记第![]() 天的利润率
天的利润率![]() ,例如
,例如![]() .
.
(1)求![]() 的值;
的值;
(2)求第![]() 天的利润率
天的利润率![]() ;
;
(3)该商店在经销此纪念品期间,哪一天的利润率最大?并求该天的利润率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国数学家布丰提出一种计算圆周率![]() 的方法——随机投针法,受其启发,我们设计如下实验来估计
的方法——随机投针法,受其启发,我们设计如下实验来估计![]() 的值:先请200名同学每人随机写下一个横、纵坐标都小于1的正实数对
的值:先请200名同学每人随机写下一个横、纵坐标都小于1的正实数对![]() ;再统计两数的平方和小于1的数对
;再统计两数的平方和小于1的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 来估计
来估计![]() 的值.已知某同学一次试验统计出
的值.已知某同学一次试验统计出![]() ,则其试验估计
,则其试验估计![]() 为______.
为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为A(A为常数)元,之后每年会投入一笔研发资金,n年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() ,
,![]() 为常数,
为常数,![]() .已知3年后总投入资金为研发启动是投入资金的3倍,问:
.已知3年后总投入资金为研发启动是投入资金的3倍,问:
(1)研发启动多少年后,总投入资金是研发启动时投入资金的8倍;
(2)研发启动后第几年投入的资金最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com