【题目】已知抛物线
的焦点为
，过焦点且斜率存在的直线
与抛物线
交于
两点，且
点在
点上方，
点与点关于
轴对称.
(1)求证：直线
过某一定点
；
(2)当直线的斜率为正数时，若以
为直径的圆过
，求
的内切圆与
的外接圆的半径之比.
科目：高中数学 来源： 题型：
【题目】对于在区间
上有意义的函数
，满足对任意的
，
，有
恒成立，厄称在上是“友好”的，否则就称在上是“不友好”的，现有函数
.
（1）若函数在区间
（
）上是“友好”的，求实数
的取值范围；
（2）若关于
的方程
的解集中有且只有一个元素，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】空气质量指数（简称：
）是定量描述空气质量状况的无量纲指数，空气质量按照大小分为六级：
为优，
为良，
为轻度污染，
为中度污染，
为重度污染，
为严重污染.下面记录了北京市
天的空气质量指数，根据图表，下列结论错误的是（ ）
A. 在北京这天的空气质量中，按平均数来考察，最后
天的空气质量优于最前面天的空气质量 B. 在北京这天的空气质量中，有
天达到污染程度
C. 在北京这天的空气质量中，12月29日空气质量最好 D. 在北京这天的空气质量中，达到空气质量优的天数有
天
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列结论：
(1)某学校从编号依次为001，002，…，900的900个学生中用系统抽样的方法抽取一个样本，已知样本中有两个相邻的编号分别为053，098，则样本中最大的编号为862.
(2)甲组数据的方差为5，乙组数据为5、6、9、10、5，那么这两组数据中较稳定的是甲.
(3)若两个变量的线性相关性越强，则相关系数
的值越接近于1.
(4)对A、B、C三种个体按3:1:2的比例进行分层抽样调查，若抽取的A种个体有15个，则样本容量为30.
则正确的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出函数
如下表，则f〔g（x）〕的值域为（ ）
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
，过点
作抛物线
的两条切线，切点分别为
，直线
的斜率为2．
（1）求抛物线的标准方程；
（2）与圆
相切的直线
，与抛物线交于
两点，若在抛物线上存在点
，使
，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
满足：
，
. （其中
为自然对数的底数，
）
（Ⅰ）证明：
；
（Ⅱ）设
，是否存在实数
，使得
对任意
成立？若存在，求出
的一个值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．
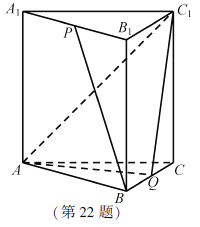
（1）求异面直线BP与AC1所成角的余弦值；
（2）求直线CC1与平面AQC1所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
