
【题目】已知函数f(x)=ex+![]() .
.
(I)当a=![]() 时,求函数f(x)在x=0处的切线方程;
时,求函数f(x)在x=0处的切线方程;
(II)函数f(x)是否存在零点?若存在,求出零点的个数;若不存在,请说明理由.
【答案】(1)y=-3x-l.(2)见解析
【解析】分析:(I)求得函数的导数![]() ,得
,得![]() ,即可利用直线的点斜式方程得到切线的方程;
,即可利用直线的点斜式方程得到切线的方程;
(II)由函数的解析式,分类![]() 和
和![]() 讨论,其中当
讨论,其中当![]() 时,利用导数求解函数的单调性与最值,即可得到函数零点的个数.
时,利用导数求解函数的单调性与最值,即可得到函数零点的个数.
详解:(I)f(x)=ex+![]() ,f'(x)=ex-
,f'(x)=ex-![]() ,f' (0)=1-
,f' (0)=1-![]() .
.
当a=![]() 时,f'(0)=-3. 又f(0)=-1,则f(x)在x=0处的切线方程为y=-3x-l.
时,f'(0)=-3. 又f(0)=-1,则f(x)在x=0处的切线方程为y=-3x-l.
(II)函数f(x)的定义域为(-![]() ,a)
,a)![]() (a,+
(a,+![]() ).
).
当x∈(a,+![]() )时,ex>0,
)时,ex>0,![]() >0,所以f(x)=ex+
>0,所以f(x)=ex+![]() >0,
>0,
即f(x)在区间(a,+∞)上没有零点.
当x∈(-∞,a)时,f(x)=ex+![]() =
=![]() ,
,
令g(x)=ex(x-a)+1,只要讨论g(x)的零点即可.
g'(x)=ex(x-a+1),g'(a-1)=0.
当x∈(-∞,a-1)时,g'(x)<0,g(x)是减函数;
当x∈(a-1,a)时,g'(x)>0,g(x)是增函数,
所以g(x)在区间(-∞,a)上的最小值为g(a-1)=1-ea-1.
当a=1时,g(a-1)=0,所以x=a-1是f(x)的唯一的零点;
当a<l时,g(a-1)=1-ea-1>0,所以f(x)没有零点;
当a>l时,g(a-1)=1-ea-1<0. 所以f(x)有两个零点.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=![]() .
.
证明:平面ADE⊥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
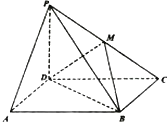
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(2x-x2)ex
①(-![]() ,
,![]() )是f(x)的单调递减区间;
)是f(x)的单调递减区间;
②f(-![]() )是f(x)的极小值,f(
)是f(x)的极小值,f(![]() )是f(x)的极大值;
)是f(x)的极大值;
③f(x)没有最大值,也没有最小值;
④f(x)有最大值,没有最小值.
其中判断正确的是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱BCF﹣ADE的侧面CFED与ABFE都是边长为1的正方形,M、N两点分别在AF和CE上,且AM=EN.
(1)求证:平面ABCD⊥平面ADE;
(2)求证:MN∥平面BCF;
(3)若点N为EC的中点,点P为EF上的动点,试求PA+PN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点P(2,0).
,点P(2,0).
(I)求椭圆C的短轴长与离心率;
( II)过(1,0)的直线![]() 与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com