练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱柱中，面为矩形，为的中点，与交于点.

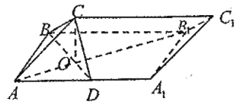
    （Ⅰ）证明：；

    （Ⅱ）若，求BC与平面ACD所成角的正弦值.

    【答案】（1）证明略（2）.

    【解析】

    试题解析：（Ⅰ）证明：由已知得，, ∴Rt△BAD∽Rt△ABB1

    ∴∠BDA=∠B1AB, ∴∠ABD+∠B1AB=∠ABD+∠BDA=90

    ∴在△AOB中，∠AOB=180 -（∠ABO+∠OAB ） =90,即BD⊥AB1

    另BC⊥AB1，BD∩BC=B，∴AB1⊥平面BCD，CD平面BCD,

    ∴CD⊥AB1

    （Ⅱ） 在Rt△ABD中，AB=1，AD= ∴AO=

    在Rt△AOB中, 得BO=, 即 ----8分

    建立如图坐标系，设BC与平面ACD所成的角为

    设平面ADC的法向量为n.解得n=.

    即BC与平面ACD所成角的正弦值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在五棱锥中，平面,∥，∥，∥，, ，，是等腰三角形．

    （1）求证：平面平面；

    （2）求侧棱上是否存在点，使得与平面所成角大小为，若存在，求出点位置，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题：直线与圆有两个交点；命题：.

    （1）若为真命题，求实数的取值范围；

    （2）若为真命题，为假命题，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“五点法”画函数在某一个周期内的图象时，列表并填入了部分数据，如下表：

    ωx＋φ

    0

    π

    2π

    x

    Asin（ωx＋φ）

    0

    5

    －5

    0

    （1）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；

    （2）将图象上所有点向左平行移动个单位长度，得到的图象，求的图象离原点O最近的对称中心.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水(单位：千克) 清洗该蔬菜千克后, 蔬菜上残留的农药(单位：微克) 的统计表：

    （1）在下面的坐标系中, 描出散点图, 并判断变量与的相关性；

    （2）若用解析式作为蔬菜农药残量与用水量的回归方程, 令,计算平均值与,完成以下表格(填在答题卡中) ,求出与的回归方程.( 精确到)

    （3）对于某种残留在蔬菜上的农药,当它的残留量低于微克时对人体无害, 为了放心食用该蔬菜, 请

    估计需要用多少千克的清水清洗一千克蔬菜？(精确到,参考数据)

    (附：线性回归方程中系数计算公式分别为；

    , )

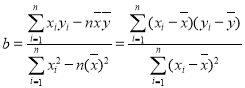    查看答案和解析>>

    科目：高中数学 来源： 题型：

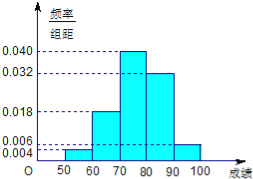
    【题目】某班50名学生在一次数学测试中，成绩全部介于50与100之间，将测试结果按如下方式分成五组：第一组[50，60），第二组[60，70），…，第五组[90，100].如图所示是按上述分组方法得到的频率分布直方图.

    （Ⅰ）若成绩大于或等于60且小于80，认为合格，求该班在这次数学测试中成绩合格的人数；

    （Ⅱ）从测试成绩在[50，60）∪[90，100]内的所有学生中随机抽取两名同学，设其测试成绩分别为m、n，求事件“|m﹣n|＞10”概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一对父子参加一个亲子摸奖游戏，其规则如下：父亲在装有红色、白色球各两个的甲袋子里随机取两个球，儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球，父子俩取球互相独立，两人各摸球一次合在一起称为一次摸奖，他们取出的三个球的颜色情况与他们获得的积分对应如下表：

    所取球的情况

    三个球均为红色

    三个球均为不同色

    恰有两球为红色

    其他情况

    所获得的积分

    180

    90

    60

    0

    （1）求一次摸奖中，所取的三个球中恰有两个是红球的概率；

    （2）设一次摸奖中，他们所获得的积分为，求的分布列及均值（数学期望）；

    （3）按照以上规则重复摸奖三次，求至少有两次获得积分为60的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义在上的奇函数，当时，（其中，是自然对数的底数，＝2.71828…）.

    （Ⅰ）求的值；

    （Ⅱ）若时，方程有实数根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足.

    （1）求证：数列是等比数列，并求的通项公式；

    （2）记数列的前项和，求使得成立的最小整数.

    查看答案和解析>>

    同步练习册答案