
 ,数列{xn}满足x1=1,xn+1=f(xn),n∈N*
,数列{xn}满足x1=1,xn+1=f(xn),n∈N* 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
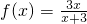 ,数列{xn}满足x1=1,xn+1=f(xn),n∈N*
,数列{xn}满足x1=1,xn+1=f(xn),n∈N*查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求P点轨迹C的方程;
(2)A、B为曲线C上的两点,F(0,![]() ),且
),且![]() (m∈R),求∠AOB(O为坐标原点)的最大值.
(m∈R),求∠AOB(O为坐标原点)的最大值.
(文)已知函数f(x)=xn+1(n∈N*,x≠0).
(1)讨论函数f(x)图象的对称性,并指出其一条对称轴或一个对称中心;
(2)令an=f′(x),求数列{an}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省名校高三数学单元测试:数列(解析版) 题型:解答题
 ,数列{xn}满足x1=
,数列{xn}满足x1=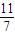 ,xn+1=f(xn);若bn=
,xn+1=f(xn);若bn=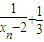 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com