
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若存在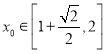 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)求出导数![]() ,计算
,计算![]() ,由点斜式写出切线方程并整理成一般式;
,由点斜式写出切线方程并整理成一般式;
(2)求出![]() ,由
,由![]() ,可得
,可得![]() 有两个满足题意的不等实根,由二次方程根的分布可得
有两个满足题意的不等实根,由二次方程根的分布可得![]() 的范围;
的范围;
(3)由(2)求出两极值点,确定![]() 的单调性,得
的单调性,得![]() 在
在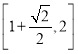 单调递增,因此题设中
单调递增,因此题设中![]() 使不等式成立,取
使不等式成立,取![]() 为最大值
为最大值![]() ,使之成立即可。化简为不等式
,使之成立即可。化简为不等式![]() 对任意的
对任意的![]() 恒成立,引入函数
恒成立,引入函数![]() ,由导数研究此函数的单调性得不等式成立的条件.
,由导数研究此函数的单调性得不等式成立的条件.
解:![]() 当
当![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
化简得:![]()
![]() 对函数求导可得,
对函数求导可得,![]()
令![]() ,可得
,可得![]()
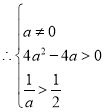 ,解得
,解得![]() 的取值范围为
的取值范围为![]()
![]() 由
由![]() ,解得
,解得![]()
而![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
![]()
![]() 在
在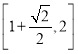 单调递增
单调递增
![]() 在
在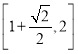 上,
上,![]()
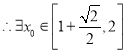 ,使不等式
,使不等式![]() 对
对![]() 恒成立
恒成立
等价于不等式![]() 恒成立
恒成立
即不等式![]() 对任意的
对任意的![]() 恒成立
恒成立
令![]() ,则
,则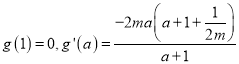
①当![]() 时,
时,![]() 在
在![]() 上递减
上递减
![]() 不合题意
不合题意
②当![]() 时,
时,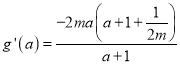
![]()
若![]() ,即
,即![]() 时,则
时,则![]() 在
在![]() 上先递减
上先递减
![]()
![]() 时,
时,![]() 不能恒成立
不能恒成立
若![]() 即
即![]() ,则
,则![]() 在
在![]() 上单调递增
上单调递增
![]() 恒成立
恒成立
![]() 的取值范围为
的取值范围为![]()


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物商场分别推出支付宝和微信“扫码支付”购物活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用“扫码支付”.现统计了活动刚推出一周内每天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次,统计数据如下表所示:
表示每天使用扫码支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据散点图判断,在推广期内,扫码支付的人![]() 次关于活动推出天数
次关于活动推出天数![]() 的回归方程适合用
的回归方程适合用![]() 来表示,求出该回归方程,并预测活动推出第
来表示,求出该回归方程,并预测活动推出第![]() 天使用扫码支付的人次;
天使用扫码支付的人次;
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 | 现金 | 会员卡 | 扫码 |
比例 |
|
|
|
商场规定:使用现金支付的顾客无优惠,使用会员卡支付的顾客享受![]() 折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受
折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .现有一名顾客购买了
.现有一名顾客购买了![]() 元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
参考数据:设![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: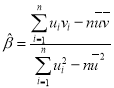 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
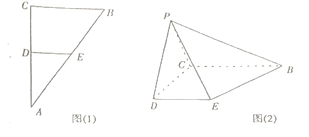
(1)求证:BC⊥PC;
(2)若BC=2CD=4,求点D到平面PBE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的展开图如图二,其中四边形
的展开图如图二,其中四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com