
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (b,c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b,c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(1)现从抽取的6件合格产品中再任选2件,求选中的2件均为优等品的概率;
(2)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
根据所给统计量,求y关于x的回归方程.
附:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: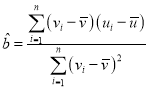 ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
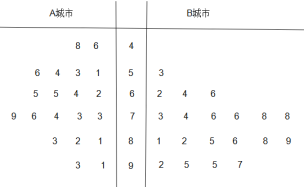
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方式“不认可”.
(Ⅰ)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关?
认可 | 不认可 | 合计 | |
A城市 | |||
B城市 | |||
合计 |
(Ⅱ)在样本A,B两个城市对此教育机构授课方式“认可”的用户中按分层抽样的方法抽取6人,若在此6人中任选2人参加数学竞赛,求A城市中至少有1人参加的概率.
参考公式: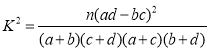 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]()
![]() 这三个条件中任选一个,补充在下面问题中,并给出解答.
这三个条件中任选一个,补充在下面问题中,并给出解答.
设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,________,
,________,![]() ,若对于任意
,若对于任意![]() 都有
都有![]() ,且
,且![]() (
(![]() 为常数),求正整数
为常数),求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为△ABC的重心G.
在底面ABC上的射影为△ABC的重心G.
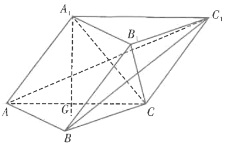
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)已知平面![]() 与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角
与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过抛物线
过抛物线![]() 的焦点,且与该抛物线交于
的焦点,且与该抛物线交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的长是16,
的长是16,![]() 的中点到
的中点到![]() 轴的距离是6,
轴的距离是6,![]() 是坐标原点,则( ).
是坐标原点,则( ).
A.抛物线![]() 的方程是
的方程是![]() B.抛物线的准线方程是
B.抛物线的准线方程是![]()
C.直线![]() 的方程是
的方程是![]() D.
D.![]() 的面积是
的面积是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com