
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上的动点,当
上的动点,当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】试题分析:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,根据离心率和在
,根据离心率和在![]() 中余弦定理,列出方程,求得
中余弦定理,列出方程,求得![]() ,即可得到椭圆的方程;
,即可得到椭圆的方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立方程组,求得则
,联立方程组,求得则![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,在由点到直线的距离公式,求得点
,在由点到直线的距离公式,求得点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即可得到三角形面积的表达,再利用基本不等式,即可求解面积的最大值.
,即可得到三角形面积的表达,再利用基本不等式,即可求解面积的最大值.
试题解析:
(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,
,
因为椭圆![]() 的离心率为
的离心率为![]() ,
,
所以![]() .①
.①
在![]() 中,
中, ![]() ,由余弦定理,
,由余弦定理,
得 ,
,
得![]() ,
,
得![]() ,
,
即![]() ,
,
所以![]() .
.
因为![]() 的面积
的面积![]() ,
,
所以![]() ,即
,即![]() .②
.②
又![]() ,③
,③
由①②③,解得![]() ,
, ![]() ,
, ![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
联立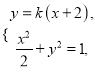
得![]() ,
,
由![]() ,得
,得![]() .
.
则![]() ,
, ![]() .
.
由弦长公式,得![]()
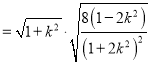 .
.
又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]()
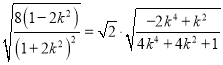
![]() .
.
令![]() ,则
,则![]() .
.
所以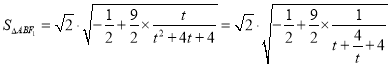
![]() ,
,
当且仅当![]() ,即
,即![]() ,
, ![]() 时取等号.
时取等号.
所以![]() 面积的最大值为
面积的最大值为![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】设![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,给出下列四个命题正确的是( )
,给出下列四个命题正确的是( )
A.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
B.![]() 平面
平面![]()
C.三棱锥![]() 的体积为定值;
的体积为定值;
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0<p1<p2<![]() ,则( )
,则( )
A. E(ξ1)<E(ξ2),D(ξ1)<D(ξ2)
B. E(ξ1)<E(ξ2),D(ξ1)>D(ξ2)
C. E(ξ1)>E(ξ2),D(ξ1)<D(ξ2)
D. E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数![]() (
(![]() ),现已知相距36
),现已知相距36![]() 的
的![]() 、
、![]() 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和
两处配置两架无人机干扰源,其对敌干扰的强度分别为1和![]() (
(![]() ),它们连线段上任意一点
),它们连线段上任意一点![]() 处的干扰指数
处的干扰指数![]() 等于两机对该处的干扰指数之和,设
等于两机对该处的干扰指数之和,设![]() (
(![]() ).
).
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() ,
,![]() 时,试确定“干扰指数”最小时
时,试确定“干扰指数”最小时![]() 所处位置.
所处位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用合适的方法表示下列集合,并说明是有限集还是无限集.
(1)到A、B两点距离相等的点的集合
(2)满足不等式![]() 的
的![]() 的集合
的集合
(3)全体偶数
(4)被5除余1的数
(5)20以内的质数
(6)![]()
(7)方程![]() 的解集
的解集
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设随机变量ξ服从正态分布N(0,1),则下列结论正确的是( )
①P(|ξ|<a)=P(ξ<a)+P(ξ>-a)(a>0);②P(|ξ|<a)=2P(ξ<a)-1(a>0);③P(|ξ|<a)=1-2P(ξ<a)(a>0);④P(|ξ|<a)=1-P(|ξ|≥a)(a>0).
A. ①② B. ②③
C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上,许多人研究过圆锥的截口曲线.如图,在圆锥中,母线与旋转轴夹角为![]() ,现有一截面与圆锥的一条母线垂直,与旋转轴的交点
,现有一截面与圆锥的一条母线垂直,与旋转轴的交点![]() 到圆锥顶点
到圆锥顶点![]() 的距离为
的距离为![]() ,对于所得截口曲线给出如下命题:
,对于所得截口曲线给出如下命题:
①曲线形状为椭圆;
②点![]() 为该曲线上任意两点最长距离的三等分点;
为该曲线上任意两点最长距离的三等分点;
③该曲线上任意两点间的最长距离为![]() ,最短距离为
,最短距离为![]() ;
;
④该曲线的离心率为![]() .其中正确命题的序号为 ( )
.其中正确命题的序号为 ( )
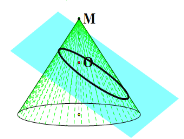
A. ①②④B. ①②③④C. ①②③D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
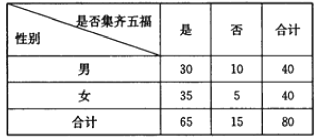
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式: 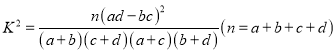 .
.
附表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com