
本小题12分)命题p: 函数y= 在(-1, +
在(-1, +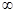 )上单调递增, 命题
)上单调递增, 命题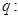 函数y=lg[
函数y=lg[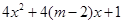 ]的定义域为R
]的定义域为R
(1) 若“ 或
或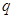 ”为真命题,求
”为真命题,求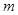 的取值范围;
的取值范围;
(2) 若“ 或
或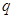 ”为真命题,“
”为真命题,“ 且
且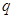 ”为假命题,求
”为假命题,求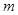 的取值范围
的取值范围
(1) m>1; (2) 1<m<2或m 3.
3.
解析试题分析:命题P真则根据对称轴和定义域的关系得到a的范围。
命题q真则真数的值域包含所有的正实数?判别式大于0求出a的范围;
据p且q为假命题?命题p和q有且仅有一个为真.求出a的范围
解: p真:  , 得m
, 得m 2; q真:
2; q真:  , 解得1<m<3.
, 解得1<m<3.
(1) m>1; (2) p, q一真一假. 因此,  或
或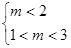 , 解得: 1<m<2或m
, 解得: 1<m<2或m 3.
3.
考点:本题主要考查了命题的真值,以及二次不等式的恒成立问题,和二次函数的单调性的运用。
点评:解决该试题的关键是解决二次不等式恒成立问题常结合二次函数的图象列出需要满足的条件、复合命题的真假与构成其简单命题真假的关系.


科目:高中数学 来源: 题型:解答题
(本题满分16分) 本题共有3个小题,第1小题满分7分,第2小题满分7分,第3小题满分2分.
设直线 交椭圆
交椭圆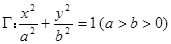 于
于 两点,交直线
两点,交直线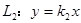 于点
于点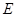 .
.
(1)若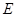 为
为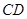 的中点,求证:
的中点,求证: ;
;
(2)写出上述命题的逆命题并证明此逆命题为真;
(3)请你类比椭圆中(1)、(2)的结论,写出双曲线中类似性质的结论(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设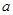 是实数,对函数
是实数,对函数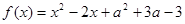 和抛物线
和抛物线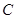 :
: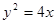 ,有如下两个命题:
,有如下两个命题: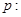 函数
函数 的最小值小于0;
的最小值小于0;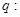 抛物线
抛物线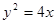 上的点
上的点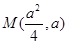 到其准线的距离
到其准线的距离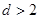 .
.
已知“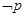 ”和“
”和“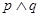
 ”都为假命题,求
”都为假命题,求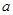 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com