已知函数y=f(x),x∈R满足f(x)=af(x-1),a是不为0的实常数.
(1)若当0≤x≤1时,f(x)=x(1-x),求函数y=f(x),x∈[0,1]的值域;
(2)若当0≤x<1时,f(x)=x(1-x),求函数y=f(x),x∈[n,n+1),n∈N的解析式;
(3)若当0<x≤1时,f(x)=3x,试研究函数y=f(x)在区间(0,+∞)上是否可能是单调函数?若可能,求出a的取值范围;若不可能,请说明理由.
【答案】
分析:(1)、配成完全平方利用配方法求值域;
(2)、根据f(x)=af(x-1)逐步利用当0≤x<1时,f(x)=x(1-x),
表示出1≤x<2,2≤x<3,3≤x<4,,…n≤x<n+1上的解析式;
(3)、由第二问得到f
n(x)=a
n•3
x-n,根据a的正负分类分别研究单调性,我们知道每一段上为单调函数,
但整个定义域上不一定单调,若单调增(减),只需每一段的最大(小)值小(大)于等于下一段的最小(大)值即可.
解答:解:(1)∵
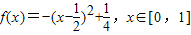
,∴
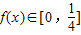
.
(2)当n≤x≤n+1(n≥0,n∈Z)时.,f
n(x)=af
n-1(x-1)=a
2f
n-1(x-2)=…=a
nf
1(x-n),
∴f
n(x)=a
n(x-n)(n+1-x).
(3)当n≤x≤n+1(n≥0,n∈Z)时,f
n(x)=af
n-1(x-1)=a
2f
n-1(x-2)=…=a
nf
1(x-n)
∴f
n(x)=a
n•3
x-n显然f
n(x)=a
n•3
x-n,x∈[n,n+1],n≥0,n∈Z,
当a>0 时是增函数,此时∴f
n(x)∈[a
n,3a
n]
若函数y=f(x)在区间[0,+∞)上是单调增函数,则必有a
n+1≥3a
n,解得a≥3;
当a<0时,函数y=f(x)在区间[0,∞)上不是单调函数;
所以a≥3.
点评:本题考查了求函数值域,函数解析式,函数的单调性,用到了配方法求函数值域,
利用f(x)=af(x-1)恒等式逐步求每段上的解析式,
特别注意分段函数,当每一段上单调,整个定义域上不一定单调,要单调,要比较相邻段上的最值大小.

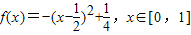 ,∴
,∴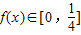 .
.

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为