练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图(1)，△ABC是等腰直角三角形，AC＝BC＝4，E、F分别为AC、AB的中点，将△AEF沿EF折起，使A1在平面BCEF上的射影O恰好为EC的中点，得到图(2)．

    (Ⅰ)求证：EF⊥A1C；

    (Ⅱ)求三棱锥F－A1BC的体积．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•成都一模）如图1，△ABC是边长为6的等边三角形，
    CD
    =
    1
    3
    CA
    ，
    BE
    =
    1
    3
    BA
    ，点G为BC边的中点，线段AG交线段ED于点F．将△AED沿ED翻折，使平面AED丄平面BCDE，连接AB、AC、AG形成如图2的几何体．
    （I）求证：BC丄平面AFG
    （II）求二面角B-AE-D的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1，△ABC的三边长分别为AC=6、AB=8、BC=10，O′为其内心；取O′A、O′B、O′C的中点A′、B′、C′，并按虚线剪拼成一个直三棱柱ABC-A′B′C′（如图2），上下底面的内心分别为O′与O；
    （Ⅰ）求直三棱柱ABC-A′B′C′的体积；
    （Ⅱ）直三棱柱ABC-A′B′C′中，设线段OO'与平面AB′C交于点P，求二面角B-AP-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）如图1，△ABC在平面α外，AB∩α=P，BC∩α=Q，AC∩α=R，求证：P，Q，R三点共线．
    （2）如图2，空间四边形ABCD中，E，F分别是AB和CB上的点，G，H分别是CD和AD上的点，且EH与FG相交于点K．求证：EH，BD，FG三条直线相交于同一点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-12,△ABC中,DE∥BC,AD∶DB=1∶2,则下列结论中错误的是(    )

    图1-12

    A.=                                    B.=

    C.=                    D.=

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年广东汕头市高二10月月考数学试卷（解析版） 题型：选择题

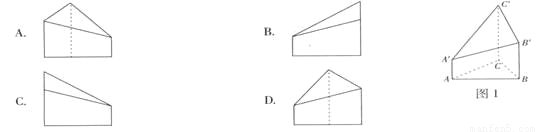
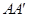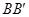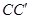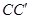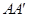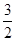
    如图1，△ ABC为三角形，// // ,  ⊥平面ABC 且3== 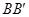=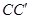AB,则多面体△ABC -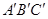的正视图（也称主视图）是（      ）

     

     

    查看答案和解析>>

    同步练习册答案